Jánossy Lajos:        Elõszó
M. Zemplén Jolán: Eötvös Loránd
Egyed László:        Eötvös Loránd tudományos eredményei a fizika és a geofizika szemszögébõl
Bibliográfia

Eötvös Loránd halálának 50. évfordulója alkalmából megjelenõ megemlékezés cikkeinek egy része a nagy tudós életrajzi adatait is részletezõ pályafutását ismerteti, a többi avatottan részletezi a tudományos munkásság világraszóló eredményeit.

Az elõszó írójának számára ennek ellenére maradt egy - az emlékezések egyikébe sem illeszthetõ - téma, amelyrõl hasznos megemlékezni ebben a kötetben is. Eötvös Loránd munkásságának nagy részében - miként errõl Egyed professzor tanulmánya is megemlékezik - a tehetetlen és nehéz tömegek közötti összefüggéseket vizsgálta.

Helyesnek látszik megemlékezni arról, hogy a modern fizika fejlõdését miként segítik Eötvös munkájának eredményei.

A közölt tanulmányból láthatja majd az olvasó, hogyan sikerült Eötvösnek - módszereinek akkoriban szinte hihetetlen finomítása után - egy a százmillióhoz arányított pontossággal bebizonyítania, hogy a tehetetlen tömeg arányos a nehéz tömeggel.

Eötvös munkáját tanítványa, RENNER János fejlesztette tovább, és egy tízes faktorral sikerült az eredeti eredményt megjavítania. Csak évekkel késõbb, Amerikában, a modern technika összes vívmányait felhasználva, javította Dicke az eredeti eredményt egy további tízes faktorral. Ezek az eredmények mutatják, hogy a tehetetlen és nehéz tömeg közötti arányosság egyike a legpontosabban megismert természettörvényeknek.

Az Eötvös által megfogalmazott és igazolt természet-törvénynek messzemenõ következményei vannak a modern elképzelésekkel kapcsolatosan. A törvény jelentõségét Einstein ismerte fel, és azt az általános relativitáselmélet megalapozásánál elméletének egyik pilléreként használta fel.

Messzemenõ jelentõségére akkor derül fény, ha a múlt századbeli felfogásoktól eltérõen figyelembe vesszük, hogy nemcsak a szokványos részecskék rendelkeznek tömeggel, hanem az elektromágneses és másfajta mezõképpen úgyanyagnak tekinthetõk, mint a részecskék, melyek ezeknek a mezõknek hordozói.

Lássuk ezt egy egyszerû példán: Az elektron az atomoknak egy alkatrésze. Az elektronnak tömege van, e tömeg a hidrogénatom tömegének kb. kétezred része és azonkívül e - az úgynevezett elemi töltésnek megfelelõ - negatív elektromos töltést hordoz. Az elektromos töltés elektromos mezõt hoz létre, tehát az e töltésû és m tömegû elektront elektromos mezõ veszi körül, amely nagy távolságokra is kiterjed.

Ha az elektronra egy F erõ hatást gyakorol, akkor az - Newton törvénye szerint - gyorsítja az elektront, úgy, hogy egy

gyorsulás jön létre, ahol m az elektron tehetetlen tömege.

Mi történik azonban az elektromos mezõvel? Az elektromos mezõt az elektron magával viszi, és ha az erõ megszûnése után az elektron v sebességgel halad, bizonyos idõ eltelte után az elektront körülvevõ mezõ szintén ugyanazzal a sebességgel követi az elektront.

Mi történik azonban abban az idõszakban, amikor az erõ hat és az elektron gyorsul?

Fel lehetne tételezni, hogy az elektromos mezõ hozzá van tapadva a töltéshez, és merev testként követi az elektront. Szemléletes módon ezt úgy lehetne elképzelni, hogy a mezõ erõvonalai, a sündisznó tüskéihez hasonlóan erednek a töltésbõl, és az elektron ezt az egész rendszert magával viszi. A valóságban (egy) ehhez hasonló folyamat megy végbe, mégis egy kis különbséggel.

Az elektron valóban úgy viselkedik, mintha a mezõ az elektronok folytatása volna. Az egész rendszer egy elasztikus testhez hasonlítható. Ha egy elasztikus test egy részét mozgásba hozzuk, a mozgás csak bizonyos idõ lefolyása után terjed ki az egész testre. Illusztrációként ehhez is egy egyszerû példa:

Képzeljünk el valamilyen szilárd anyagból, például acélból készült rudat. Ha a rudat mozgásba hozzuk, úgy hogy egyik végét megnyomva azt hosszirányba toljuk, akkor az elsõ benyomásunk az, hogy a nyomásnak engedve az egész rúd azonnal elmozdul. Valójában a folyamat komplikáltabb. Amikor a nyomás a rúd egyik végére nehezedik, közvetlen eredményként csak egy vékony felületi réteget hoz mozgásba, és a rúd végét kicsit összenyomja. Ez a következõ réteget hozza mozgásba, és az egymást követõ rétegek egymás után mozdulnak el mindaddig, amíg a mozgás az egész acélrúdra kiterjed.

E folyamat eléggé nehézkesen írható le, de a valóságban rendkívül nagy sebességgel folyik le. Technikai terminológiát használva azt mondhatjuk, hogy a rúd végére nehezedõ nyomás elasztikus hullámot indít a rúdban, és ezen elasztikus hullám hatására az egész rúd mozgásba jön.

Az elasztikus hullám sebessége a rúdban néhány km/sec, és így könnyen kiszámítható, hogy egy 1 m hosszú acélrúd egészén egy ezredmásodpercnél rövidebb idõ alatt terjed el a mozgás.

Ha az elektront elmozdítjuk, az elmondotthoz hasonló módon elasztikus hullámként terjed ki a mozgás az egész mezõre, azonban a terjedési sebesség ebben az esetben a fénysebesség, tehát 300 ezer km/sec. A mozgás a mezõben így rendkívül rövid idõ alatt terjed, és sok vonatkozásban úgy viselkedik, mintha a mezõ azonnal követné az elektron mozgását. A mozgásnak ez a látszólagos egyidejûsége nagyobb mértékû, mint a szilárd testeknél.

Az energiaviszonyokra vonatkozóan szükséges még egy megjegyzés. Ha egy rudat, mint a fent említett példában, eltolunk, elsõ pillanatban csak egy vékony réteget hozunk mozgásba, és így csak annyi munkát végzünk, ami a vékony réteg elmozdításához szükséges. Azonban a keletkezõ elasztikus hullámok, amelyek a mozgást az egész rúdra kiterjesztik, visszafelé is hatnak, és így megnehezítik a feladatot. Végeredményben a toló erõnek nemcsak az elsõ réteg tehetetlenségét kell leküzdenie, hanem az elasztikus hullámok által létrejövõ ellenállást is, és ily módon a kifejtendõ összerõ felnõ arra az értékre, amely az egész rúd mozgásbahozatalához szükséges.

Az egész komplikált folyamat tehát egy nagyon egyszerûen érthetõ eredményt hoz létre. Ha egy rudat mozgásba kívánunk hozni, akkor olyan erõt kell kifejtenünk, mint ami az elsõ látszatnak megfelelõen az egész rúd tehetetlenségének legyõzéséhez szükséges. Megjegyzésünk csak azt kívánja érzékeltetni, hogy ezt az egyszerû eredményt egy nagyon komplikált belsõ fizikai folyamat hozza létre.

Az elektron kérdéséhez visszatérve, ott is éppen errõl van szó. Ha magát az elektront elmozdítjuk, az elektront körülvevõ mezõt mozgásba hozó hullámok, elektromágneses hullámok, és ezek egy bizonyos mértékben fékezik az elektront. Ennek a komplikált folyamatnak eredményeként azt mondhatjuk, hogy a töltést körülvevõ mezõ valóban hozzájárul az elektron tehetetlen tömegéhez, vagyis a mezõ maga is tehetetlen tömeggel rendelkezik.

További kérdésként merül fel, hogy vajon az elektront körülvevõ elektromágneses mezõ a tehetetlenségi tömeg mellett rendelkezik-e nehéz tömeggel is? Másképpen kifejezve, hozzájárul-e az elektront körülvevõ mezõ az elektron súlyához, és a két elektron közötti tömegvonzást vizsgálva, hozzájárul-e a tömegvonzáshoz a mezõnek megfelelõ tömeg?

Amennyiben az Eötvös-féle törvény pontosan érvényes, biztosra kell vennünk, hogy ez valóban így van. Hiszen az anyag atomokból áll, az atomok elektronokat és más töltött részecskéket tartalmaznak. Ha egy atomokból álló anyagot gyorsítunk, akkor a gyorsító erõknek a mezõk visszahatása által létrejött ellenállást, pontosan úgy kell leküzdeniök, mint a részecskék tömegének tehetetlenségét, és így egy atomokból álló anyag tehetetlenségi tömegét mérve, automatikusan mind a részecskék tehetetlenségi tömegét, mind az õt körülvevõ mezõ tehetetlenségi tömegét mérjük. Különbözõ atomoknál a részarány a részecskék tehetetlenségi tömege és a mezõkben elraktározott tehetetlenségi tömeg között változhat.

Minthogy azonban az elektromágneses mezõben raktározott tehetetlenségi tömeg igen kicsi, ezért nagyon pontos mérésekre van szükség annak megállapítására, hogy a mezõben raktározott tömeg pontosan úgy viselkedik-e, mint a részecskék nyugalmi tömege.

A legújabb mérések pontossága elegendõnek látszik ahhoz, hogy ezt a következtetést alátámassza. Tehát kísérletekbõl következtethetünk arra, hogy egy elektromágneses mezõ éppen olyan módon rendelkezik gravitációs tulajdonságokkal, mint a szokványos anyagok.

Azt a tényt, hogy a mezõk éppen úgy rendelkeznek gravitációs hatással, mint a szokásos értelemben vett tömeg, már Eötvös kisebb pontossággal végzett kísérleteibõl is meg lehetett állapítani, azonban a fent leírtnál kevésbé közvetlen módon.

Az atommagok úgynevezett nukleonokból vannak felépítve, vagyis protonokból és neutronokból. Ha egy proton és egy neutron egyesül, egy úgynevezett deuteron jön létre. Ennek a tömege azonban kisebb, mint a rész tömegek összege. Tehát

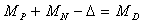
ahol M_P, M_N és M_D-vel a proton, neutron és deuteron tömegét neveztük el, pedig az úgynevezett tömegdefektus, vagyis az a tömeg, amelyik "elveszett" az egyesülés folytán. Köztudott ma már, hogy a tömeg egyáltalában nem veszett el, hanem a proton és neutron egyesülésekor sugárzás jött létre, a sugárzásmezõ pedig a mennyiségû tömeget magával vitte.

Felmerül tehát a kérdés, hogy a sugárzás által elszállított tömeg tehetetlenségi vagy nehézségi tömeg-e - avagy mindkettõ. A mérések azt mutatják, hogy a sugárzás egyenlõ mértékben vitt magával tehetetlenségi és nehézségi tömeget.

A különbözõ elemek tudniillik atom-magokat tartalmaznak, és a különbözõ atomok magjai más-más tömegdefektussal rendelkeznek.

Ugyanakkor - és ezt már Eötvösnek sikerült pontosan kimutatnia - a legkülönbözõbb atomfajtákból felépített anyagok ugyanabban az arányban tartalmaznak tehetetlen és nehéz tömegeket, és ez világosan bizonyítja, hogy a tömegdefektusnak megfelelõ anyagnak tehetetlenségi és nehézségi hatása ugyanabban az arányban van, mint az atommagokban megmaradó anyagnak.

A részletek ismertetése nélkül még megjegyezzük azt a - az Eötvös kísérletekbõl következõ - megállapítást, hogy nemcsak részecskék, hanem az anyag atomjait összetartó, vagy az anyag részecskéivel kölcsönhatásban levõ legkülönbözõbb mezõk pontosan olyan természetûek, mint azok a részecskék, amelyek az atomok építõkövei. Ez a felfogás lassan alakult ki, de egyre nagyobb jelentõségûvé válik a modern fizikában. Helyességének egyik legfõbb bizonyítéka éppen az Eötvös-féle törvény, amelynek így a modern fizikai felismerésekre is jelentõs hatása van.

																JÁNOSSY LAJOS
																akadémikus

1848. július 27. Ha több mint 120 esztendõ távlatából visszatekintünk erre a napra, a szabadságharc még dicsõséges napjai jutnak eszünkbe. Maga a név: Eötvös pedig talán a többséget báró Eötvös Józsefre, a liberális politikusra, a haladó szellemû íróra, a társadalmi haladás szolgálatába állított irányregények és néhány felejthetetlenül szép vers szerzõjére emlékezteti. A fizikus számára azonban - nemcsak itthon, hanem külföldön is - az Eötvös név még más fogalmakkal is kapcsolatos: Eötvös-törvény, Eötvös-állandó, eötvös-egység, Eötvös-hatás, Eötvös-kísérlet, Eötvös Loránd Fizikai Társulat, Eötvös Loránd Geofizikai Társulat, Eötvös Loránd Tudományegyetem... törvények, egység, intézmények õrzik Eötvös Loránd nevét. A nemzetközi tudományos gyakorlatban a legnagyobb megtiszteltetés, ha egy-egy tudósról törvényt, hatást, egységet neveznek el. Ki ne ismerné a volt, watt vagy amper elnevezéseket? Az ohmegység Georg Simon Ohm, a Faraday-törvények, a Faraday-effektus, az elektrolízis Faraday-féle törvényei, a kapacitás farad nevû egysége pedig a nagy angol kísérletezõ, Faraday nevét õrzik stb.

1848. július 27-én Eötvös József budai házában Rosty Ágnes a legnagyobb és nemzetközileg is legjelentõsebb magyar fizikusnak, Eötvös Lorándnak adott életet.

Tulajdonképpen semmi valószínûsége sem volt annak, hogy ezen a napon Eötvös József házában éppen egy jövendõ fizikus szülessék. Mind a nemzeti, mind a családi hagyományok ellentmondtak ennek. A magyarországi fizika történetében arisztokrata tudóst keveset találunk, lényegében egyet sem, mert aki - mint például Bethlen Miklós a XVII. században - foglakozik is külföldi egyetemi tanulmányai során fizikával, matematikával, késõbb inkább a politika felé fordul. A XVIII. században a piarista tanárok között találunk bárót és fizikust, ez azonban inkább arra jellemzõ, hogy hazánkban még a XIX. században is túlnyomórészt egyházi emberek mûvelték a matematikát és fizikát. Jedlik Ányos is, Eötvös Loránd elõdje a Pesti Egyetem kísérleti fizika tanszékén, bencés szerzetes volt.

Eötvös Loránd 1860-ig otthon tanult, majd a piaristák pesti gimnáziumában fejezte be tanulmányait. Természetesnek látszott, hogy a fiatal Eötvös jogászhallgató lett, bár tanult magánúton matematikát Petzval Józsefnek, a híres bécsi magyar fizikusnak az öccsétõl, Petzval Ottótól, aki a Pesti Egyetemen, majd a Mûegyetemen a matematika és a mechanika tanára volt. Jogi tanulmányai mellett természettudományos tárgyakat hallgat, sõt dolgozik Than Károlynak, a neves fizikokémikusnak a laboratóriumában is.

Magyarországon már a XVI. századtól kezdve, sõt elõbb is, szinte elengedhetetlen követelmény volt, hogy a tudományos pályára készülõ fiatalemberek tanulmányaikat részben vagy egészben valamelyik külföldi egyetemen végezzék. Az egyetem a kor s a felekezet szerint az idõk folyamán változott, de a tény maga változatlan maradt. A középkorban Párizs, Padua, Bologna, Róma, Krakkó, Prága egyetemein tanultak a magyar diákok, a reformáció után a protestánsok számára Wittenberg, Halle, Jena, Heidelberg, valamint a svájci és holland egyetemek kerültek elõtérbe. Eötvös Loránd korában azonban már elsõsorban az volt a döntõ, hol, milyen neves tanárok tanítanak. Így került Eötvös 1867-ben Heidelbergbe, ahol az akkori idõk legnevesebb professzorai: Gustav Kirchhoff (1824-1887), Hermann Helmholtz (1821-1894) s Robert W. Bunsen (1811-1899) tanítottak.

E három professzor mindegyikérõl külön tanulmányt lehetne írni, szerepük a fizika történetében - nemcsak mint pedagógusoké, hanem mint alkotó fizikusoké is - olyan jelentõs. Kirchhoff nevét talán legjobban a róla elnevezett áramelágazási törvényekbõl ismerjük. Kirchhoff azonban Bunsennel - akinek nevét a kémia története is nagy megbecsüléssel õrzi - közösen nem kevesebbet alkotott meg, mint a színképelemzést. Végül Helmholtz, a nagy fiziológus, az energia megmaradás elvének propagálásával tette nevét halhatatlanná.

E professzoroktól Eötvös Loránd elsõsorban a fizikát tanulta meg. Nem követte egyiket sem valamelyik speciális területén. Ifjúkori legjelentõsebb eredménye, az Eötvös-törvény felfedezése is inkább Than Károlyra, elsõ kémikofizikus mesterére utal, mint Bunsenre. Egy azonban kétségtelen, hogy Eötvös Heidelbergben sajátította el a precíz kísérletezésnek azt a mûvészetét, amely ma is kivívja a kísérleteit megismételni óhajtó szakemberek csodálatát.

A fiatal Eötvös pályaválasztása nem volt probléma nélküli. Nyilvánvalóan szerepet játszott ebben származása mellett - amely számára mint egy parancsoló szükségszerûséggel írta volna elõ a politikusi, államférfiúi pályát - a fizika akkori helyzete. Eötvös József és Loránd 1866-70-es levelezésébõl bár eléggé szûkszavúan, de mindkét probléma szempontjából kaphatunk annyi felvilágosítást, hogy több-kevesebb biztonsággal felvázolhatjuk az ifjú Eötvös késõbbi életútjának alakulását meghatározó mozzanatokat. E levelezés tehát - némileg merész extrapolálással - választ ad a következõ kérdésekre: 1. miért lett Eötvös fizikus, 2. (ezt már elmosódottabbnak látjuk) miért éppen azokat a területeit választotta a fizikának, amelyeket mûvelt. S végül ebben a levelezésben már megmutatkoznak azok a hatások is, amelyek eredményeképpen Eötvös Loránd mint pedagógus, kultúrpolitikus s mint tudományszervezõ is beírta nevét a magyar mûvelõdéstörténet és az oktatás történetébe.

Nézzük elõször a pályaválasztás kérdését. Eötvös Józsefet fiatalkori hajlamai késõbbi érdeklõdési iránya, a tudomány, a filozófia felé vonzották. A magyar történelem, közélet azonban a politikai élet középpontjába sodorta. A kiegyezés utáni politikai helyzet kevéssé tette rokonszenvessé a politikai pályát Eötvös József elõtt, így hát nem meglepõ, hogy örömmel fogadja fia ötletét: életét a tudománynak óhajtja szentelni. Íme apa és fiú levelezésébõl két, talán a legjellemzõbb és egyben legdöntõbb részlet: 1866. március 28-án írja apjának, még külföldi útja elõtt: "Az ambíció és a kötelességérzet... velem született, e két indulatot kielégíteni és pedig kielégíteni úgy, hogy emellett egyéni függetlenségemet megtartsam: élet célom, és legalább eddig úgy találtam, hogy annak leginkább úgy felelhetek meg, ha tudományos pályára lépek." S egy évvel késõbb, 1867. márc. 24-én, amikor pályaválasztása egyelõre eldöntöttnek látszik, írja az apa: "...valóságos megnyugvásomra szolgál, hogy más pályán látlak. Haladj bátran elõre, és ne sajnáld fáradságodat. A tudomány körében a legnagyobb erõfeszítés eléri jutalmát, mert azt nem várja az emberektõl, hanem magában a tudományban találja." Talán elsõsorban ezek a szavak kísérték végig Eötvös Lorándot egész életében. Számára a tudományos munka jutalma valóban mindig maga a tudomány maradt.

Ennek ellenére a pályaválasztás már említett problémája más forrásokból is fakad. Amikor az ifjú Eötvös Heidelberg után Königsbergbe kerül, az ott mûvelt elméleti fizika átmenetileg visszariasztja nemcsak a fizikától, hanem még a laboratóriumi, kutatói pályától is. Ebben kétségtelenül része volt a korabeli fizika helyzetének is. Igaz, valamivel késõbb történt, hogy Jolly, a neves kísérleti fizikus azt mondta Max Plancknak, hogy a fizika - 1880 táján - már kész, befejezett egész, ami hátra van, már csak néhány konstans pontosabb kiszámítása... fiatalember tehát nem adhatja fejét elméleti fizikára.

Eötvös Königsbergben - feltehetõleg - úgy érezte, hogy az ott ûzött elméleti fizika meddõ, kilátástalan, s megtanulni nagyon nehéz. Ez indította arra, hogy egy Petermann nevû tudós által vezetett északi-sarki expedícióhoz akart csatlakozni. Úgy gondolta, hogy egy ilyen vállalkozás során megtalálja tudományos ambícióinak kielégítését anélkül, hogy az elméleti fizikai tudományok kásahegyén keresztül kellene rágnia magát. Bizonyára szerepet játszott azonban az az - akkor még rejtett - vágy is, hogy a Földrõl minél többet megtudjon.

Ismét a bölcs apának kellett közbelépnie: a tudományos szempontból bizonytalan kimenetelû, de rendkívül költséges expedícióról nemcsak szorult anyagi helyzetére való hivatkozással beszéli le a fiát, hanem rámutat: kezdõ fiatalember komoly tudományos eredményt egy ilyen expedíció tagjaként nem produkálhat. Ugyanakkor - humán mûveltségû tudós volta ellenére - világosan megmutatja fiának: ha nem tetszik, akkor is ott kell maradnia Königsbergben a félév végéig. Eötvös József nem helyeselte a korabeli elméleti fizika és matematika "metafizikus" irányzatait, mondván: "Ismered nézeteimet azon irányról, melyet a német tudósoknak egy része a természettudományokban követ, s mely a fizikát mindinkább a metafizika körébe vezeti. Nincs helyén, s nem is érzem magamat irányodban kompetensnek, hogy ezen irányról hosszabban szóljak, de ha nem kétlem is, hogy szintén egyes nagy lépések történhetnek a természet ismeretében, általában nem tartom ezen irányt termékenynek, s úgy vagyok meggyõzõdve, hogy még sokáig a természettudományok az indukció és experimentum útján fogják tenni a legnagyobb lépéseket." (Kiemelés tõlem. Z. J.) Pontosan nem világos, milyen irányzatokra célzott itt Eötvös József, feltehetõ azonban, hogy többek közt a korban olyan divatos étermodellekrõl volt szó, amelyekkel Weber és követõi, többek közt Kirchhoff is foglalkoztak, valamint talán azokra a törekvésekre, amelyekkel az elektromos és gravitációs hatások terjedését igyekeztek elméletileg igazolni. Természetesen szó lehetett más, ma már elfelejtett elméletekrõl is.

Eötvös Loránd átmeneti megtorpanása nem sokáig tartott. Lemondott az északi-sarki expedícióról, de arról nem, hogy fizikai kutatásai tárgyává magát a Földet tegye meg. A késõbbiekben még részletesen sor kerül Eötvös - a Földdel kapcsolatos - kutatásainak ismertetésére, itt talán mégis érdemes idézni Eötvös saját szavait, amelyeknek õszinte lelkesedése azt mutatja, hogy késõbbi tudományos munkásságában megtalálta mindazt, amit a kalandvágyó, de még kissé határozatlan ifjú az életben keresett. 1901-ben akadémiai elnöki megnyitójában saját gravitációs vizsgálatairól és az általa feltalált torziós ingáról ezeket mondja: "A középkor elõítéleteinek és csodaszereinek lomtárából elõkerestem a varázsvesszõt, s azt nem imádsággal, nem is ördöngõsséggel, hanem a vesszõhöz, melyrõl a varázs az idõk folyamán amúgy is lekopott, jobban illõ mechanikai érvelésekkel arra bírtam, hogy feleletet adjon. Az igaz, hogy nem arra kértem, hogy rejtett kincseket mutasson; arra sem, hogy ellenségeimet, ha vannak, megjelölje; csak azt kívántam tõle: engedjen bepillantani annak az erõnek rejtélyeibe, amely e földön mindent mozgat, mindennek kijelöli a helyét." - Majd a torziós inga leírása után: "Egyszerû, mint Hamlet fuvolája, csak játszani kell tudni rajta, s úgy, mint abból a zenész gyönyörködtetõ változatokat tud kicsalni, úgy ebbõl a fizikus a maga nem kisebb gyönyörûségére kiolvashatja a nehézségnek legfinomabb változásait..." És, utalásként az ifjúkori kalandvágyra és arra, hogy ezt a vágyat sikerült - talán az eredeti elképzelésnél is jobban - kielégítenie: "Azzal a kíváncsisággal, mellyel az utazó ismeretlen vidékre jutván, annak hegyeit és völgyeit kutatja, jártam én is a Balatonon. Az én ismeretlen vidékem ott feküdt mélyen a jég tükre alatt, nem láttam és nem is fogom látni soha, csak eszközöm érezte meg, és mégis milyen nehezen váltam el tõle... Amikor onnét eljöttem, s különösen, amikor megfigyelésem adatait rendezve az ilynemû kutatások helyességérõl meggyõzõdtem, akkor egy új és nagyobb vállalkozás terve érlelõdött meg agyamban. Itt lábaink alatt terjed el hegyek koszorújától övezve az Alföld rónasága. A nehézség azt lesimítván, kedve szerint formálta felületét. Vajon milyen alakot adott neki? Micsoda hegyeket temetett el és mélységeket töltött ki lazább anyaggal, amíg létrejött az az arany kalászokat termõ, magyar nemzetet éltetõ róna? Amíg rajta járok, amíg kenyerét eszem, erre szeretnék még megfelelni." Ez a beszéd akkor hangzott el, amikor Eötvös már mintegy 15 éve foglalkozott a gravitációval kapcsolatos tudományos problémákkal.

Igaz, kora divatját követve, elõzõleg õ is tett egy halvány kísérletet, hogy a távolbahatást - egyelõre az elektromosság könnyebbnek látszó területén - igazolja. Errõl szól 1877-es akadémiai felolvasása. Ez azért rendkívül jellemzõ Eötvös tudományos egyéniségére, mert egyrészt megmutatja, hogy már ebben a - történetileg aránylag korai - idõpontban átlátta a mechanikai szemlélet elégtelenségét minden természeti jelenség magyarázatára, másrészt rámutat arra, hogy az igazi tudósnak le kell mondania a "végsõ" igazság megtalálásáról: "Bármennyire is fejlõdjenek tehát fizikai elméleteink, mégis mindig oly feltevésekre fognak támaszkodni, melyek tovább nem bizonyíthatók... Az igazi természettudós... tudja, hogy osztályrészeül a természet végokaival szemben a lemondás jutott, de azért nem csügged el, mint Faust, ki véges munkáért végtelen jutalmat követel, hanem ernyedetlenül halad elõre az elérhetetlen cél felé, s örömet talál magában a kutatásban s azokban az eredményekben, melyeket az emberiség anyagi jólétének elõmozdítására értékesít."

Persze túlzás és hamis aktualizálás lenne ezeknek a szavaknak alapján Eötvös Lorándot a dialektikus materializmus hívének feltüntetni, hiszen világos, hogy ennek ellenére a távolbahatás elemzése során lényegében csupán odáig jutott el, mint Newton, hogy a gravitáció kérdésérõl nem érdemes hipotéziseket alkotni. Pedig hivatkozik is Maxwell 1873-ban megjelent Treatise on Electricity and Magnetism c. fõmûvére mint Newton óta a legjelentékenyebb próbálkozásra, amellyel igyekezett "...a két pont közötti erõkifejtést a közbensõ anyagban tovaterjedõ mozgásokból magyarázni". Eötvös azonban Maxwell munkáját is a német fizikai iskola, Weber, Kirchhoff stb. meddõ kísérletei közé sorolja, amikor így folytatja: "De mi volt a nyereség? Az eredeti feltevés helyett még összetettebb feltevések azon anyagot illetõen, mely a hatás továbbvitelére szolgáljon." Fiatalkori idegenkedése a Königsbergben ûzött elméleti fizikától döntõ maradt további tudományos érdeklõdése szempontjából, és így a maxwelli elektrodinamika mindvégig idegen maradt tõle, ezért a következõ konklúzióhoz jut: "Végre is meg kell tehát nyugodnunk abban, hogy a tudomány nem adja a természeti tüneményeknek feltétlenül igaz magyarázatát, hanem csak közelebb vezet ahhoz a határhoz, ahol a megfoghatatlan kezdõdik."

Így vált Eötvös a klasszikus fizika utolsó nagy képviselõjévé, de oly módon - amint a fentiekbõl láthattuk -, hogy tisztában volt e fizika alapjait alkotó mechanisztikus szemlélet korlátaival. Hû maradt mintaképéhez, Galileihez és Newtonhoz anélkül, hogy a "newtonisták" követõinek túlzásaiban osztozott volna.

Itt kissé elébevágtunk az eseményeknek, midõn nemcsak az Eötvös pályaválasztásával kapcsolatos átmeneti nehézségeket vázoltuk, hanem arra is rámutattunk, hogy e nehézségek leküzdése után milyen típusú tudós vált Eötvösbõl, hogyan lett kora egyik legjelentékenyebb kísérletezõje és az elsõ olyan magyar tudós és professzor, akinek munkássága nemzetközi elismerésben is részesült.

1870. július 8-án, alig 22 éves korában doktorált Eötvös Heidelbergben a Kirchhoff, Bunsen és Königsberger professzorokból álló bizottság elõtt summa cum laude eredménnyel, amint azt még e napon büszkén jelenti apjának, írván, hogy az elért fokozat "...sokak által irigyelt megtiszteltetés. Ezen felül feljogosít egy munka benyújtása és egy halom formalitás teljesítése után az egyetemi docentúrára. E fokozatot itt nemigen osztogatják; ha jól vagyok értesülve, ebben a félévben kívülem még csak egy jelöltnek adatott, s kultuszminiszteri örömed telhetik abban, hogy ez is magyar volt... Neve König Gyula, gyõri születésû - matematikus". Az életre szóló barátság majd szoros együttmûködés König Gyulával a hazai matematika és fizika elõbbrevitelére tehát már a heidelbergi években kezdõdött.

Eötvös Loránd azonban nem Heidelbergben, hanem Pesten folyamodott magántanári képesítésért 1871-ben. Habilitációs dolgozata még azt a próbálkozást tükrözi, hogy a rezgési elméletbõl levezesse a távolbahatást, amelynek kilátástalanságát a már idézett 1877-es tanulmányában is sejtette. Eötvös József már nem érte meg, hogy fia végképp elindult azon a pályán, amelyen legszívesebben látta, mert 1871. február 2-án meghalt. Eötvös Lorándot a bölcsészkar ugyanezen év március 14-én habilitálja, sõt kinevezi a felsõbb természettan helyettes tanárává. Ezt csakhamar, 1872. május 10-én követi nyilvános rendes tanári kinevezése, egyelõre az elméleti fizika tanszékére; ez az elmondottak szerint tulajdonképpen nem felelt meg Eötvös Loránd tudományos egyéniségének, mert bár disszertációja, habilitációs dolgozata elméleti tárgyú, elsõ - jelentõs tudományos munkája a kapillaritásról már a kiforrott kísérletezõt mutatja. Ezért 1874-tõl résztvesz a kísérleti fizikai elõadások tartásában is, végül 1878-ban, Jedlik Ányos nyugalomba vonulásakor átveszi a Kísérleti Fizika Tanszéket és azt több mint 30 évig tartja meg, 1919-ben bekövetkezett haláláig, csupán 1894-ben válik meg katedrájától rövid idõre, amikor át kell vennie a kultuszminiszteri tárcát.

E rövid politikai szereplése mellett Eötvös egész életét a tudományos kutatás, a tanítás és a tudomány szervezése töltötte ki. A Természettudományi Társulatban 1870 óta választmányi tag, 1872-tõl "A természettudományi rovat" vezetõje, 1880-tól alelnöke. Elõadásaival, cikkeivel, javaslataival igyekezett a hazai tudományos ismeretterjesztést elõsegíteni. A Magyar Tudományos Akadémia már 1873-ban levelezõ tagjának, 1883-ban rendes tagjának választotta, 1889-tõl pedig az Akadémia elnöki tisztségét viseli egészen 1905-ben történt lemondásáig.

A fent jelzett dátumokhoz kapcsolódik azután Eötvös Loránd egész tudományos és közéleti tevékenysége. Egy-egy nagyobb tudományos felfedezésérõl mindig elõször az MTA III. Osztályának számol be. Itt mutatja be az Eötvös-törvényt, itt számol be gravitációs és földmágneses vizsgálatairól, de ugyanakkor szívén viseli a fizika, általában az oktatásnak az ügyét nemcsak az egyetemen, hanem a középiskolában is. Ez utóbbinak eredménye az egyetem, a Természettudományi Társulat és az Akadémia mellett a negyedik - talán számára legkedvesebb - mûködési terület, az általa alapított mathematikai és Physikai Társulat.

Eötvös Loránd tehát majdnem félszázadon át mûködött mint tudós, pedagógus és tudományszervezõ. Ez a félévszázad nemcsak egyetlen emberi életnek hihetetlen szellemi gazdagságát tükrözi, hanem kitörölhetetlen nyomot hagyott hazánk tudományának, oktatásának és egész mûvelõdésének történetében.

Ha sorra vesszük Eötvös különbözõ tevékenységeit, nem vagyunk könnyû helyzetben: egyéniségében és életében ugyanis a kutató tudós, a pedagógus és a tudománypolitikus olyan szerves egészé fonódik, hogy jóformán minden tette és megnyilatkozása jellegzetesen csak az igazi tudósé, az igazi tanáré és a nemzete mûvelõdését állandóan szívén viselõ politikusé lehet.

Igen nagy lelkesedéssel fogott hozzá tanári munkájához. Elméleti fizikai elõadásainak tartalmáról egyelõre nem sokat tudunk, de feltehetõ, hogy e téren heidelbergi és königsbergi tapasztalatait hasznosította. Tudományos dolgozatainak és fennmaradt litografált jegyzeteinek alapján azonban feltehetõ, hogy ezek az elõadások ugyanolyan szigorúan logikus felépítésûek voltak, mint minden egyéb munkája.

Igazi területe azonban mind a tudományos kutatás, mind az oktatás terén a kísérleti fizika volt. Elõdje, Jedlik Ányos az elsõ volt a Pesti Egyetemen, aki igyekezett kora színvonalán, megfelelõ demonstrációval kísérleti fizikát tanítani. Bármilyen tisztelettel adózunk is azonban Jedlik Ányos emlékének, kétségtelen, hogy céljának elérésében a legkülönbözõbb objektív és szubjektív tényezõk akadályozták. Az objektív tényezõkre nem kell túl sok szót vesztegetni. Jedlik 1838-tól 1878-ig volt a Pesti Egyetem professzora. Kinevezése elõtt már megpróbálta a gyõri, majd pozsonyi Akadémiát kísérleti eszközökkel felszerelni, jóformán sikertelenül. Amikor talán már tudott volna némi eredményt elérni, közbejött a 48-49-es szabadságharc, utána pedig az elnyomás évei. Ezekben az idõkben egy pesti professzornak bizony nehéz volt megszereznie a szertár fejlesztéséhez szükséges dotációt. Tudjuk, hogy Jedlik többnyire saját zsebébõl pótolta a hiányzó összegeket, és persze még így sem sikerülhetett neki korszerû demonstrációs felszerelést elérnie. A szubjektív akadályok más forrásból fakadtak. Jedlik kitûnõ kísérletezõ volt. Jelentõs felfedezései, találmányai: a szódavízgyártás, a rácsosztógép, a különféle elektromos berendezések - köztük az elektrotechnikát késõbb forradalmasító dinamó - mind erre mutatnak. Ugyanakkor arra sem ideje, sem - talán - képessége nem volt, hogy kora fizikájának vezetõ elveit áttekintse. 1850-ben megjelent egyetemi tankönyvének óriási érdeme, hogy többé-kevésbé összefoglalta benne a mechanikát, bár azt is kissé elavultan, de éppen a legújabb, legnagyobb jelentõségû felfedezések hiányoznak belõle, illetve nem tudjuk, hogy mit írt volna kora hõtanáról, fénytanáról, ha elkészül a mû második kötete. Õ ugyanis csak a "súlyos testek" természettanáról írt, amelyben a mechanika mellett elsõsorban kémia és akusztika van, s a hõtan és fénytan mellett az elektromosságtan is hiányzik. Ezek képviselték ugyanis e korban a "súlytalan" anyagokat (hõanyag, fényanyag, elektromos és mágneses folyadékok, mind a múlt század továbbélõ örökségei).

Eötvös tehát kettõs feladattal találta magát szemben, amikor 1878-ban a Pesti Egyetem Kísérleti Fizika Tanszékét véglegesen átvette. Tartalmilag a kor színvonalának megfelelõ elõadást adni hallgatóinak, és felszerelni a szertárat úgy, hogy a bemutatott kísérletek megfelelõen támasszák alá az elõadásokat.

Sajnálatos módon Eötvös tankönyvet nem írt. Feltehetõleg azért nem - a minden valószínûség szerint fennálló idõhiánytól eltekintve -, mert a minden munkájára olyan jellemzõ lelkiismeretesség és mûgond mellett nem érezte még az elõadások tartalmát eléggé kiforrottnak. Így a magyar tankönyv-irodalomban Jedlik egykötetes könyve és a következõ (a Tangl-féle, aki egyébként Eötvös tanítvány volt) egyetemi fizika tankönyv között csupán Eötvös néhány fennmaradt litografált jegyzete hidalja át az ûrt. Ezekbõl a jegyzetekbõl, valamint elõadási kísérleteibõl, amelyeket szintén tanítványai jegyeztek fel, kaphatunk képet Eötvösrõl, a tanárról. A fennmaradt jegyzetek természetesen nem adhatnak teljesen hû képet Eötvös elõadásairól, hiszen a jegyzet leírójának - helyenként esetleg hiányos - képességeit is tükrözik, annyit azonban megállapíthatunk, hogy igen logikus, abban a korban feltétlenül modern és legteljesebb mértékben kísérleti elõadásokról volt szó, és tulajdonképpen már nem lett volna túl nagy munka ezekbõl tankönyvet készíteni. Idézzük talán Mikola Sándor, a közvetlen tanítvány jellemzését: "...Eötvös a nagy igazságok embere. Ezeket nem mint készeket nyújtja, hanem a jelenségekbõl hüvelyezi ki. Elõadásait a mélyreható analizáló szellem hatja át. A természeti tüneményeket a bennük megnyilatkozó hatók elemeire bontja szét, és azon igyekszik, hogy tanítványait a fogalmaknak, gondolatoknak és törvényeknek legutolsó, többé már nem elemezhetõ részeihez vezesse el, oda, ahonnan a formáktól, sablonoktól mentes tudás ere fakad. Nem ismerünk a fizikai irodalomban mûvet, amelyre az analizáló szellem annyira rányomta volna a bélyegét, mint az õ elõadásaira. Ítélete elfogulatlan, gondolatmenetének minden állítását igyekszik valódi értékben feltüntetni, és megmutatni, hogy törvényeink mennyire közelítik meg az igazságot. Valamely kedves hipotézis vagy a rendszer, vagy a pedagógiai hatás kedvéért soha sem enged az igazságból egy szemernyit sem."

Az elõadás valóban klasszikus rendben felépített: kísérleti fizika, mechanika, szilárd, cseppfolyós és légnemû testek fizikája, hõtan, mágnesség, elektromosság, hang- és rezgéstan, (geometriai és fizikai) fénytan. Az idõközben megjelent tankönyvek egészen a legújabb idõkig - Tangl, Pogány, Gyulai - általában ezt a beosztást tükrözik, talán annyi eltéréssel, hogy a hangtant és rezgéstant a mechanika után helyezik el. Elõadásának bevezetésében Eötvös kifejti, hogy minden tudományt különbözõ, esetleg véletlenszerû szempontok szerint lehet rendszerezni. Ilyen rendszerezést nyújt pl. a szótár. A természettudományokban azonban evvel ellentétben "...nem mellékes tulajdonságokból, hanem oly sajátságok szerint, amelyek a jelenetek lényegét képezik". "A rendezés alapját ... az ún. tapasztalati törvények képezik." Önmagában azonban a tapasztalat, "az észleletek" még nem elegendõek a természet megértéséhez, így például a csak észlelésre szorítkozó csillagászatnak is szüksége van a mechanika elméleti törvényeire, alkalomadtán pedig hipotéziseket is kell átmenetileg alkalmaznia. Kísérleti tudomány és elmélet szoros kapcsolata indokolja, hogy a fizikát mechanikával kell kezdeni. Eötvös saját közvetlen érdeklõdése tûnik ki abból, hogy milyen fejezeteket tárgyal aránylag nagyobb részletességgel: így a nehézségi erõ kérdésének általában, a gravitációs állandó meghatározásának, a csavarási rugalmasságnak, illetve a csavarási ingának elég nagy teret szentel; ugyanígy a kapillaritás és földmágnesség tárgyalása túlmegy a jegyzet egyéb fejezeteinek részletességén. Kétségtelen, hogy a rendelkezésre álló nem túl áttekinthetõ szerkezettel leírt jegyzetbõl a kísérleti fizika alapjait ma is meg lehetne tanulni, különösen akkor, ha a hallgatóknak módjukban volna az elõadást hallgatni és a gondosan felépített kísérleteket végignézni.

Nincsenek adataink arra nézve, mennyi idõ alatt sikerült Eötvösnek intézete demonstrációs anyagát olyan gazdaggá tenni, mint amilyen volt. 1919 után a következõ világháborúig nem sok fejlesztés történt, úgyhogy a 20-as és 30-as évek orvos, gyógyszerész és matematika-fizika tanár szakos hallgatói lényegében még az eredeti, Eötvös által tervezett kísérleti berendezéseket láthatták. (A baj az, hogy a fizika fejlõdésének megfelelõen nem láttak többet!) Sok eredeti, Eötvös által kigondolt kísérletet még ma is alkalmazunk az egyetemen, fõiskolákon és a középiskolában egyaránt.

Eötvös kísérleteire a szellemes egyszerûség mellett a kvantitatív igazolásra törekvõ precizitás jellemzõ, éppúgy, mint tudományos berendezéseire.

A szabadesés törvényének igazolására és a g egyszerû mérésére vezette be Eötvös azt az ingakísérletet, amelynél a félperces lengésidejû inga 490 cm-es rúdja mellett egy golyó éppen az inga végére helyezett kis kosárba esik.

A matematikai inga rezgéseinek színuszos voltát (kis kilengéseknél) szintén szellemes szerkezet mutatja. A festett vízzel telt csõ alatt az inga alatt kis kocsi húzható el a lengésekre merõlegesen. Ugyanolyan szinusgörbét kapunk, mint a rezgõ hangvilla és kormozott üveglapból álló közismert kísérlet esetében.

A tömeg, tömegmérés, tömegvonzás állandójának mérésével kapcsolatos kísérleteket különös gonddal szerkeszti meg. Laboratóriumi gyakorlatba illõ pontossággal tanítja meg hallgatóit a mérlegelésre (kémiai elõképzettsége is kitûnik ebbõl) és egy eredeti módszerre a mérleg érzékenységének meghatározására. Eötvös már korán egyszerû berendezéssel mutatta ki a tömegvonzást torziós ingával. A torziós inga tükrérõl visszaverõdõ fénysugár jelezte a nyugalmi helyzetet, ennek elmozdulása az ingarúd mellé vitt 13 kg-os ólomsúly jelenlétét. Ilyen finom torziós eszköz készítése persze igen költséges volt, mert az inga lengõje még platinából is készült. Eötvösnek ezt az eszközt is sikerült egy egyszerûbb, de elõadási célokra megfelelõ szellemes kísérlettel helyettesítenie, amelyben ólomlemezek és higannyal telt lapos korongok közt lép fel kimutatható vonzóerõ.

Messzire vezetne minden egyes ötletes kísérlet ismertetése. Természetesen nem mind volt eredeti, egy részük már a klasszikus irodalomból ismert. Eötvös azonban rendszerint ezeken is kisebb-nagyobb változtatásokat hajtott végre, hogy a jelenségeket minél meggyõzõbben mutathassa be. A lényeg az, hogy egész elõadását úgy szõtték át a kísérletek, hogy azok a tartalmi mondanivalónak mindig szerves részei voltak.

Nyilvánvaló, hogy Eötvös rendkívül nagy munkát fektetett elõadásainak felépítésébe, intézete megszervezésére, felszerelésére. Nem csoda, hogy némi csalódással kellett tapasztalnia, hogy a Pesti Egyetemen nem találkozik a hallgatóságnak azzal a lelkesedésével és tudásvágyával, amelyet Heidelbergben kollégáinál tapasztalt, és amely õt magát is fûtötte egyetemi évei alatt.

1887-ben, tizenötéves egyetemi oktatási tapasztalatai alapján nyílt levélben fordul Trefort Ágoston vallás- és közoktatásügyi miniszterhez Néhány szó az egyetemi tanítás kérdéséhez címen. Az abban feltárt problémák egy része nemcsak Eötvös korában volt probléma, hanem az maradt az egész Horthy korszakon keresztül, és csak a felszabadulás után nyert megoldást, más része - sajnos - még ma is megoldásra vár. Eötvös elmondja itt, hogy elméleti fizikai elõadásait kisszámú hallgatóság elõtt tartotta, nem törödve szabályzatokkal "...abban a hitben éltem, hogy a jó tanár bármilyen szabályzatok mellett is sikert arathat". Mikor azután nagyszámú hallgatóság elõtt kellett kötelezõ tantárgyat elõadnia, már más tapasztalatokat szerzett. Keserû kifakadása nemcsak egy gyakori helyzetet tár fel, hanem azt is mutatja, milyennek tartotta Eötvös a jó tanárt: "Mennyire leverõ e tapasztalat a tanárra nézve, mennyire bénítja ez munkaerejét, arról csak annak lehet fogalma, aki meggondolja, hogy a lelkiismeretes tanár egészen elõadásában él, arra gondol, avval foglalkozik az egész tanév ideje alatt, s így amikor annak végén arról gyõzõdik meg, hogy hallgatói nem követték, elkeseredve kénytelen bevallani, hogy életébõl újra egy évet elfecsérelt eredménytelenül. Pedig az egyetemi tanár életét talán még többre becsüli, mint mások; mert széppé teszi azt neki a tudomány varázsa." A következõ mondatot olykor néhány mai vizsgáztató is leírhatta volna: "A legkeserûbb csalódás azonban vizsgálatokon vár a tanárra, a gondosan egybeállított és tudományosan átgondolt elõadások után kénytelen kérdéseit a középiskola színvonalára alászállítani, hacsak a képtelenségig következetes lenni nem akar, s a vizsgálandók 99 százalékát meg nem buktatja."

Eötvös, összehasonlítást téve a különféle külföldi egyetemi rendszerek között, ésszerû javaslatokat tesz a javításra. Ezek elemzésétõl pillanatnyilag eltekintünk, csupán az említett nyílt levél néhány olyan részletét idézzük még, amelyek Eötvös tudományos és pedagógiai elveit tükrözik: "...az egyetemnek ... kötelessége, hogy a tudomány fejlesztésével foglalkozzék, s oly tudósokat neveljen, kiknek sorából magát kiegészíteni s így fenntartani tudja. Ezért az egyetemi tanári állásra csakis a tudományos kutatások körében kipróbált, önálló gondolkozás képesíthet." Majd másutt: "Bizonyos dolog, hogy csak az lehet jó tanár, aki maga tudománnyal foglalkozik, mások eszméit is csak az képes helyesen hirdetni, akinek magának eszméi vannak." Ez a gondolat állandóan visszatér Eötvös beszédeiben és írásaiban. Tanítani az tud, aki maga is nemcsak tud, de tudós... Így például 1891-ben, rektori székfoglalójában a Treforthoz intézett levél egyik vezérgondolatát folytatja: "...annyiszor emlegettem már a tudományos iskolát, a tudományos tanítást, hogy szükségesnek látom arról is szólani, mit értek én e kifejezésben. Röviden megmondhatom. Tudományos az iskola, tudományos a tanítás ott, de csakis ott, ahol tudósok tanítanak. Hozzátehetem, hogy tudósnak nem a sokat tudót, hanem a tudomány kutatóját nevezem."

Az eddig idézett megnyilatkozások lényegében azokat az általános gondolatokat és javaslatokat tükrözik, amelyek Eötvösben több éves egyetemi és közéleti mûködése során támadtak, és amelyeknek megfelelõ alkalmakkor (természetesen sokkal többször, mint ahányszor idézhettük) kifejezést is adott.

Nyilvánvaló azonban, hogy Eötvös - egyetemes érdeklõdése ellenére - elsõsorban fizikus volt és a fizika tanára. Így 1892-ben az egyetem újjáalakításának ünnepén tartott rektori beszédében már az egyetemi fizikaoktatásról beszél. Még szabadkozik is kissé, hogy ezúttal "nem általánosabb érdekû dolgokra" fordítja figyelmét. Majd így folytatja: "...még a legáltalánosabb és legszélesebb körû kérdések megoldásához is legbiztosabban az az út vezet, melyet a részleteiben felderített igazság tûz elénk; s az, aki ezt a sokszor hosszadalmas és fáradságos utat követi, jobban megóvja magát a csalódásoktól, mint az, aki ötletszerûen kimondott általános tételek csábító szavaira hallgat."

A Bölcsészkar oktatója elõtt az (akkori) egyetemen hármas feladat állt: tudósokat képezni valamely szakban, segédtudományként adni egyes szakokat, vagy csupán az általános mûveltséget kielégíteni egy-egy szak által. "A hallgatóknak mind e három csoportja méltán kívánhatja, hogy az egyetemen megtalálja, amit keres; de azért ne gondoljuk, hogy ezért mindegyikére nézve külön-külön intézkedések volnának szükségesek. Vezessük csak valamennyit ugyanahhoz a forráshoz, a tiszta tudomány forrásához, s legyünk azon, hogy e forrásból eredõ folyónak mentén kedvvel kövessen ki-ki addig, ameddig ideje és ereje megengedi", mert: "Nem az a feladat, hogy minden hallgatónknak mást, hanem az, hogy mindegyiknek eleget adjunk." Akinek legtöbbet kell adnunk - mondja Eötvös -, a tanárjelöltek. És most újra visszatér a kedvenc gondolat, amelyet ma is meg kell szívlelnünk: "Õk (ti. a fizikus tanárjelöltek) azok, akiket e szakban tudósokká kell képezni; tudósokká mindenekelõtt azért, hogy tanítani tudjanak." Minden ellenkezõ véleménnyel szemben, amely szerint az általános mûveltséget nyújtó középiskolában nincs szükség "szaktudósokra", Eötvös ezt válaszolja: "Nem olyan mesterség az a középiskolai tanárság, melyen a tanítás módjára elõírt szabályok szolgaszerû alkalmazásával boldogulni lehetne..." "Igen, képezzük tudóssá középiskolai tanárainkat azért, hogy tanítani tudjanak, de azért is, hogy pályájokon, amely a földi javakkal, dicsõséggel és bizony még az érdemelt elismeréssel is alig kecsegtet, ne bénuljon el erejük a mindennap ismétlõdõ feladatok iránti közönyösségben, hogy legyen egy olyan foglalkozásuk is, amely varázsával mindig ébren tartsa törekvésöket..." Az egyéni életút és életcél mellett van egy általános cél is, amelyet szintén igen sokszor hallhatunk Eötvöstõl emlegetni. Ez is tudományos és emberi magatartásának egyik alapvetõ jellemvonása: "Képezzük õket tudósokká végre még azért, hogy nemzetünknek a tudomány terén munkásokat adjunk, mert bizony ezer év után, amelyet jól, rosszul e hazában töltöttünk, még sok itt a tennivaló."

Végigtekintve az eddig idézett mondatokon, ezekbõl azt szûrhetjük le, hogy aki ezeket mondta vagy leírta, bizonyára okos, nemes gondolkodású ember, de hát ezek még mindig csak szép szavak, mi lett belõlük?

Eötvös nem állt meg a szavaknál. Igyekezett véleményét tettekkel is igazolni, javaslatait megvalósítani. A német egyetemekkel való összehasonlításból azt a következtetést vonta le, hogy a sikeres egyetemi oktatás feltételei közé tartozik a hallgatóság lelkes tanulni vágyása: a tárgy iránti érdeklõdése és a jó tanárok mellett az, hogy a hallgatók mûvelt, vagyonos családok gyermekei. Legalább is ezt tapasztalta külföldön és saját életében. A liberális és demokratikus gondolkodású Eötvös József fia azonban csakhamar belátta, hogy a magyar mûvelõdés, tudósképzés sikerét nem lehet a harmadik feltételhez kötni. Ezért a gondtalan tanulást - legalább a hozzá legközelebb álló Bölcsészkaron - másképpen, az édesapjáról elnevezett Eötvös kollégium alapításával igyekezett biztosítani. Ez volt Eötvös rövid miniszterségének legnagyobb, legmaradandóbb tette. A kollégium nemcsak otthont és ellátást nyújtott az arra rászoruló tanárjelölteknek, hanem azok a legkiválóbb professzorok vezetése alatt készülhettek a tudományos pályára. Sok ma is élõ vagy nemrég elhunyt nemzetközi hírnevû tudósunk kezdte meg e kollégiumban pályáját. Az Eötvös kollégium diákjai valóban túlnyomórészt megvalósították azt az ideált, amelyet Eötvös már fiatal korában annyi lelkesedéssel tûzött maga elé, és amelynek az elérése a feladat nehézségei miatt sokszor lehetetlennek látszott.

Az Eötvös kollégium alapítása 1894-ben történt, de Eötvös már sokkal elõbb hozzáfogott másik kedvenc gondolatának megvalósításához: nemcsak tudósokká nevelni a középiskolai tanárokat, hanem azt is biztosítani, hogy a jól kiképzett tanárok tudósok is maradjanak. Ezt a célt szolgálta az Eötvös Loránd Mathematikai és Physikai Társulat alapítása 1891-ben.

Eötvös külföldrõl hazatérte után úgyszólván minden tudományos megmozdulásban részt vett mind a Természettudományi Társulatban, mind a Magyar Tudományos Akadémia III. Osztályában. Az elõbbi folyóirata, a Természettudományi Közlöny 1869-tõl, az Akadémia III. Osztálya pedig 1882-tõl közölt matematikai és természettudományi cikkeket, éppen Eötvös kezdeményezésére. Eötvös felismerte, mennyire szükséges lenne egy kizárólag a matematikával és fizikával foglalkozó társaságot és folyóiratot alapítani, amelynek célja a népszerû ismeretterjesztésnél lényegesen többet, de még nem kimondottan szûk szakmai ismereteket adni.

A Társulat magja az a kisebb, matematikusokból és fizikusokból álló csoport volt, akik Eötvös vezetése alatt eleinte fehér asztalnál, kötetlen szakmai beszélgetésekre jöttek össze: Hunyady Jenõ, König Gyula, Scholtz Ágoston, Szily Kálmán, Fröhlich Izidor, Gruber Nándor és Wittmann Ferenc. A beszélgetésekbõl lassan elõadások lettek, és Eötvös elérkezettnek látta az idõt, hogy megpróbálja az összejöveteleket szervezetté, majd hivatalossá tenni, és õ maga vállalkozott az elsõ reprezentatív elõadás megtartására. 1890. november 29-én Eötvös a következõ meghívót küldte ki említett kollégáinak és másoknak: "Uraim! A Mathematikai Társaság felszólítására december hó 4-én és 18-án esti 6 órakor a tudományegyetem physikai intézetében a földi gravitációról két elõadást fogok tartani, amelyekben az arra vonatkozó vizsgálódásaim módszereit és eredményeit bemutatni szándékozom. - Szeretném e tárgy iránt a physikával foglalkozó t. Collegáim érdeklõdését is felkelteni, mert meg vagyok gyõzõdve arról, hogy a tudományos eszmecsere az egyes kutatóknak úgy, mint a tudománynak nagy hasznára válik, s ezért kérem, vegyen részt ez összejöveteleinken. Megvallom, az a remény is kecsegtet, hogy ezzel az elsõ lépést fogjuk megtenni arra, hogy hasonló célból még többször egybegyûljünk és szorosabb érintkezésbe lépjünk. Igaz tisztelettel maradok híve b. Eötvös Loránd." A meghívottak elõtt azután Eötvös hasonló szellemben szólt a második elõadás után: a személyes érintkezés szakmai szempontból mindenkinek csak hasznára lehet: "Meggyõzõdésem pedig a következõ: vagyunk már elegen és munkakedvünk is elegendõ arra, hogy remélhetõleg létrejövõ összejöveteleink eredményeit írásba is foglaljuk, s ezáltal vidéki szaktársainkhoz, kiknek megjelenésére õszinte sajnálatunkra nem számíthatunk, szintén közelebb jutunk..." Itt vetõdik fel tehát elõször a szakfolyóirat gondolata - amint azt Eötvös a továbbiakban ki is fejti -; lelkére köti a megjelenteknek, hogy a karácsonyi ünnepek alatt gondolkozzanak a kérdésen.

Ilyen elõzmények után került sor 1891. november 5-én a Mathematikai és Physikai Társulat alakuló ülésére. A hazai matematikus és fizikus társadalom késõbbi fejlõdése szempontjából döntõ szavakkal nyitotta meg Eötvös ezt a gyûlést: "Uraim! Avégbõl jöttünk össze, hogy a Mathematikai és Physikai Társulatot megalakítsuk. Csendesen, hangzatos szavak kerülésével, éspedig a siker kilátásával tehetjük ezt, mert oly helyzetben vagyunk, mint régi szövetségesek, kik baráti szövetségöket késõbb törvényesítik. Közös cél, s annak eléréséért közös munkálkodás hozta létre szövetkezésünket, és ezért nem is szükséges, hogy újra elõadjuk az okokat, melyek bennünket a frigy megkötésére bírtak, s most annak törvényesítésére indítanak. De egy dolgot szem elõtt kell tartanunk most, amikor úgyszólván a nyilvánosság elé lépünk. Azt tudniillik, hogy most még nagyobb buzgalommal és kitartással kell önként elvállalt kötelességeink teljesítésére törekednünk. A tudomány haladását rendes összejöveteleinkben élõszóban elõadni, és mindazt, ami a szakember figyelmére méltó, szakfolyóiratunkban megírni: ez a mi feladatunk. E feladat nem látszik nagynak, alig többnek egy önképzõkör feladatánál; és mégis, ha híven teljesítjük, érdemes munkát végzünk, és nagy szolgálatot teszünk vele. Hiszen ha elérjük azt, hogy mindenki, aki hazánkban fizikát és matematikát tanít, igazán fizikus és matematikus legyen: akkor nagy szolgálatot tettünk nemcsak az iskolának, hanem hazánk tudományosságának is. Hogyha ezen önképzés feladatát híven és komolyan teljesítjük, annak az is lesz az eredménye, hogy a mi körünkbõl fognak majd kiválni a tudomány önálló mûvelõi és fejlesztõi."

"Ezzel a Mathematikai és Physikai Társulatot megalakultnak nyilvánítom."

Ugyanilyen döntõ jelentõségû, ma már klasszikussá vált sorokban hívja fel Eötvös tanártársait a Mathematikai és Physikai Lapok elõfizetésére:

"Szaktársainkhoz!

Új folyóirattal, a Mathematikai és Physikai Lapok-kal lépünk nem a nagyközönség, hanem hazánk matematikusai és fizikusai elé - avval a kéréssel, hogy olvassák s azt megírni segítsenek.

Folyóiratot akarunk teremteni, amely a mi kedves hazánkban is terjessze tudományszakainknak napról napra gyarapodó vívmányait, amely matematikusaink és fizikusaink tudományos érdeklõdését ébren tartva, kedvessé tegye nekik tudományunknak nemcsak mûvelését, de tanítását is. Azért, ha e lapokat csak magunknak írjuk is, olyan formában, amint szakember a szakembernek ír, mégis fontos szolgálatot vélünk vele tenni közmívelõdésünknek, mert kétségtelen, hogy a tanítás sikere úgy a felsõ, mint a középfokú iskolában mindenekelõtt a tanár tudományos képzettségétõl függ.

Célunk nem a tudomány népszerûsítése, s nem is önálló tudományos dolgozatok közlése: mások sikerrel vállalkoztak már e feladatok teljesítésére. Mi tudományos ismertetõ cikkek alakjában fogjuk megadni a szakembereknek azt a szellemi táplálékot, melyre szüksége van, ha haladni akar, mert jól tudjuk, hogy különösen a tudományban a nem haladás csak annyit jelent, mint az elmaradás."

A Társulat elsõ elnöke természetesen Eötvös Loránd lett, az is maradt haláláig. Eötvös javaslatára "a Társulat elsõ tagja" Jedlik Ányos lett. A Társulat második közgyûlésének megnyitója ismét Eötvös tudományszeretetérõl tanúskodik: "...Egyszerû de egészséges viszonyaink között egyszerû és kevés a Társulati ügy is. ...Arra törekszünk valamennyien, hogy tudósokká váljunk, és tudósok maradjunk, mert erõs meggyõzõdésünk, hogy az iskola, amelynek életünket szenteltük, csak abban az arányban javulhat, a technikai ipar, melynek meghonosításán fáradozunk, csak abban az arányban fejlõdhetik, amelyben tudományunk színvonalát magasabbra emelni bírjuk."

A Társulat vezetése nem volt könnyû. Állami támogatást nem kapott, a szerény tagdíjakból és az MTA évi segélyébõl tartották fenn. Ezen még Eötvös minisztersége sem változtatott. Miniszterségéhez azonban mégis egy igen fontos esemény fûzõdik: az Eötvös Loránd Matematikai és Fizikai Tanulóverseny alapítása, erre Eötvös saját zsebébõl emlékérmet is alapított. Ha ma büszkék vagyunk rá, hogy fiataljaink matematikából és fizikából külföldi, nemzetközi vetélkedõkön is megállják a helyüket, nem szabad elfelejtenünk, hogy az elsõ országos tanulmányi verseny alapítója és szervezõje éppen Eötvös Loránd volt. Azóta más és más nevek alatt, különbözõ korosztályoknak rendeztek és rendeznek tanulmányi versenyeket külön matematikából, külön fizikából, de a Mathematikai és Physikai Társulat késõi utódja, az Eötvös Loránd Fizikai Társulat most is megrendezi minden év õszén az az évben érettségizettek számára az Eötvös fizikai versenyt. E versenyek nyertesei között sok ismert tudós és mérnök nevével találkozunk, akiknek talán éppen a verseny megnyerése adott újabb lendületet a tudományos hírnév megszerzésére. A Társulat élete egyébként a versenyek évente való megrendezése mellett évi 20, késõbb 10-12 elõadás szervezésébõl és a közgyûlésbõl állt. Az elõadások legjobbjai megjelentek a Mathematikai és Physikai Lapokban is, amely nem egy ifjú tehetség számára biztosított publikációs lehetõséget, és ugyanakkor meglepõ gyorsasággal tájékoztatta a szaktársakat a fizika legújabb eredményeirõl.

És mindezen tevékenység középpontjában Eötvös állt. Az elõadásokat az õ intézetének tantermében tartották, õ teremtette meg a hiányzó pénzt, az õ buzdító szavai vezették az ifjú tudósokat, az õ fáradtságot nem ismerõ tudományos munkája szolgálhatott minden kolléga számára mintaképül. Eötvös nem is mulasztotta el soha, hogy egy-egy új felfedezésérõl a Társulat elõtt is beszámoljon.

1919-ben, Eötvös halálakor nemcsak a magyar történelemnek egy szakasza zárult le. Határkõ, szomorú határkõ volt ez a Társulat történetében is. A hálás tagtársak impozáns különszámot szerkesztettek Eötvös munkásságáról a Mathematikai és Physikai Lapokból a nagy tudós 70. születésnapjára, de ezt a szép munkát már csak a nagybeteg Eötvös láthatta, és nyomtatásban csak 1921-ben jelenhetett meg. Az ugyanebben az évben újjáalakult Társulat ekkor vette fel Eötvös Loránd nevét, majd a felszabadulás után a matematikai és fizikai részleg szétvált. Az elõbbi jelenleg Bolyai János Matematikai Társulat néven mûködik, míg az utóbbi mint Eötvös Loránd Fizikai Társulat õrzi a nagy alapító nevét és ápolja emlékét.

Eötvös 16 évig volt az MTA elnöke, 1905-ben mondott le, hogy minden idejét tudományos munkájának szentelhesse. Egyedül Elnöki beszédeibõl, nagy emberekrõl tartott megemlékezéseibõl is meg lehetne rajzolni tudományos egyéniségét. Idézzük Eötvös mûveinek talán legalaposabb ismerõjét, Selényi Pált, amint Eötvös akadémiai tevékenységét jellemzi: "Akadémiai elnöki megnyitó beszédeiben az akadémiák létjogáról, a tudomány és költészet, a tudomány és gyakorlat, a tudós és a nagyvilág, az egyéni és kollektív tudományos munka viszonyáról és még sok egyébrõl találunk értékesnél értékesebb megállapításokat; amelyeket persze minden nemzet, sõt minden nemzedék is újra és újra talál meg és önt korszerû formába, de amelyeket jórészt magyar nyelven elõször Eötvös mondott ki, és amelyeknek igazságát - egy magyar író szavát idézve - jórészt az a melegség fogja megõrizni, amivel ez igazságok kimondattak. De ennél többet is mondhatunk. Beszédeiben és minden más megnyilatkozásában Eötvös a dialektikus gondolkodás igazi mestereként mutatkozik meg. Minden dolgot minden oldalról megvilágít, kapcsolataikat felismeri, az örökös változás és az ellentéteken át történõ fejlõdés gondolatát egyaránt felleljük nála."

A századfordulón a Magyar Tudományos Akadémia elnökének nem volt könnyû dolga. A Mathematikai és Physikai Társulat elnökének csak anyagi gondjai voltak, de megértõ, segíteni kész, ugyanarra a célra törekvõ barátok vették körül. A nagyobb testületben azonban, amelynek mûködését az egész ország figyelemmel kísérhette (de nem kísérte!), szûk látókörû, reakciós politikusokkal kellett megküzdenie az anyagi eszközök hiánya mellett. Ennek eredménye volt az az elzárkózottság, amelyet Eötvös olyan keserûen emleget, de amelyet szükségszerûnek tart. Attól a politikától csak elzárkózni lehetett. Eötvös azonban tudta, hogy ez másképpen is lehetne: "Majd akkor, mikor nemzetünk jogosult vágyai Isten kegyelmébõl teljesedésbe mennek; amikor állami intézményeink azt a fejlettséget érik el, és olyan biztos alapokon nyugosznak, hogy azoknak rendezésére és megszilárdítására nem lesz, mint ma, annyi politikusra szükség, s a legjobbak helyesebb arányokban fogják szétoszthatni erõiket a nemzeti jólétet és mûvelõdést elõmozdító munkásság különbözõ terein, akkor, amikor a magyar gazdának, iparosnak, kereskedõnek, mûvésznek és tudósnak, mindegyiknek a maga módja szerint meg lesz adva a képesítés arra, hogy abban, amiben munkálkodik, nagyra vihesse, s a sokaság mûveltsége is oda fejlõdött, hogy az érdemet minden formában felismerni és méltatni tudja: akkor ebben a boldog idõben az Akadémia is megint nem százak, hanem milliók szerint fogja számíthatni barátait."

1900-ban hangzottak el Eötvösnek ezek a szavai. 19 év múlva már-már elkövetkezett ez a korszak, de Eötvös azt már nem érte meg egészségben; és rövidesen követte õt sírjába az a proletárdiktatúra is, amely mindezt meg tudta volna valósítani.

A miniszter Eötvösnek két fontos tettérõl, az Eötvös kollégium és az Eötvös verseny alapításáról már volt szó. A közoktatás egyéb terén hozott intézkedései arra mutattak, hogy méltó fia volt Eötvös Józsefnek. Nemcsak mint miniszter, hanem mint fõrendiházi tag is folytatta Eötvös harcát a vallásszabadságért, a zsidók emancipációjáért. Nagy szeretettel foglalkozott a tanítóság problémáival. Különösen érdemes kiemelni a korban teljesen szokatlan nemzetiségi politikáját: "Az iskola nemzetiségi kérdéseiben nem általános rendszabályokkal fogunk rendet teremteni, hanem azzal, hogy bár legkisebbnek látszó és sokszor nagyon lényeges esetekben kellõ tapintattal intézkedünk, és lehetõleg nem cselekszünk mást, olyat ami fájna nekünk, ha velünk történnék meg." - Ennek ellenére mégsem sajnálhatjuk, hogy nem volt tovább miniszter, mert tudományos munkássága megmaradt örök kincsünknek, míg annak a kornak a legnemesebb politikai törekvéseit, legbölcsebb intézkedéseit is elsöpörték a következõ évtizedek viharai.

Eredményekben, küzdelmekben gazdag élet után következett el 1919. április 12-e; amikor óriási gyászoló tömegtõl feketéllett a Nemzeti Múzeum környéke. Itt volt felravatalozva báró Eötvös Loránd, "a proletárhatalom nagy halottja".

Lukács György, közoktatásügyi népbiztos, aki a gyászbeszédet mondta, nevezte így azt az Eötvöst, aki azt vallotta, hogy "...csak az az igazi tudomány, amely világra szól; s ezért, ha igazi tudósok és - amint kell - jó magyarok akarunk lenni, úgy a tudomány zászlóját olyan magasra kell emelnünk, hogy azt határain túl is meglássák, és megadhassák neki az illõ tiszteletet". Lukács György így búcsúzott Eötvöstõl: "Végtelen fájdalommal és szomorúsággal tölt el bennünket az a tudat, hogy az új állam küszöbén nélkülöznünk kell Eötvös lángeszét és munkáját...", "...ki nem tekintve egyéni érvényesülést, osztályérdeket, csak a tudománynak élt, csak a tudományért küzdött, dolgozott..."

És annak a tudósnak a ravatala elõtt, akinek elõször sikerült Magyarországon a tudomány zászlóját a világszint magasságáig emelnie, Lukács György meghajtotta "a világ proletáriátusának zászlaját...".

																M. ZEMPLÉN JOLÁN

Amikor arra vállalkozunk, hogy Eötvös tudományos munkásságát jellemezzük, önkéntelenül is Scribe híres darabja, az Egy pohár víz jut eszünkbe, melyben a szerzõ a pohár víz köré építette fel az egész cselekményt. Leegyszerûsítve, egy pohár víz volt az, ami Eötvös egész érdeklõdési körét lekötötte, s ami köré alapvetõ eredményei csoportosulnak. Egy pohár víz felületét kétféle erõcsoport összhatása alakítja ki: a kapilláris erõk s a Föld felszínén észlelhetõ s mindenütt jelenlevõ nehézségi erõ, amit közvetlenül a testek súlyában észlelhetünk. Eötvös élete, munkássága és érdeklõdése - jelentéktelen kitérésektõl eltekintve - e két jelenségcsoportra összpontosult, s e két területen ért el alapvetõ eredményeket. Még a két terület vonatkozásában is szorosabb s hosszantartóbb volt a frigye a gravitációval. A hajszálcsövesség területén elért alapvetõ eredménye mintha egy kalandban feloldódott elsõ nagy szerelem lett volna, amely soha sem tért vissza életébe. Ezért mi súllyal a tömegvonzással kapcsolatos vizsgálataival fogunk foglalkozni.

Hogy a tömegvonzás jelentõségét a geofizikában alaposabban megérthessük, sokkal távolabbról kell elindulnunk. Elõször azt kell tisztáznunk, mit is értünk a Föld alakján. E fogalmat legkönnyebben fejlõdéstörténetének végigkísérésével érthetjük meg.

Az elsõ tudományosan is megalapozott eredmények a Föld alakjáról elõször a görögöknél bukkannak fel. Már idõszámításunk elõtt a hatodik században azt hirdeti Püthagorasz, hogy a Föld gömb alakú. Gondolatmenete a következõ volt: A Hold fényváltozásai akkor magyarázhatók a legegyszerûbben, ha e fényváltozásokat annak tulajdonítjuk, hogy a Nap más és más irányból világítja meg a Holdat. Miután a világos és sötét részek választóvonala, a terminator a Holdon mindig körív, geometriai megfontolásból következik a Hold gömb alakú volta. Ennek merész általánosítása már a Föld gömb alakúsága.

Közvetlen érveket a Föld gömb alakúságára késõbb Arisztotelésznél találunk, aki a holdfogyatkozást mint a Föld árnyékát értelmezte, s az árnyék méreteinek kör alakjából mondotta ki, hogy a Föld gömbhöz hasonló. De érvelését a Föld gömbölyûségének igazolására azzal a megfigyeléssel is alátámasztotta, hogy az egyes ismert csillagképek és csillagok delelési magassága annál alacsonyabb, minél északabbra utazunk.

Még egy hatalmas eredményt értek el a görögök a Földdel kapcsolatban. Õk határozták meg elõször a Föld méretét. Eratoszthenész, aki i. e. 276 és 195 között élt Alexandriában, azt vette észre, hogy a nyári napforduló idején a felsõ-egyiptomi Syene város kútjaiba délben bevilágít a Nap anélkül, hogy árnyékot vetne, a tõle északra levõ Alexandriában viszont a napsugár iránya ugyanakkor 7°-os szöget zár be a függõlegessel. Ez a szögeltérés gömb alakú Földön a két városnak a Föld középpontjától való látószögét szolgáltatja, s így a két város távolságának ismeretében a Föld sugara kiszámítható. Syene és Alexandria 5000 stadionra volt egymástól, így a Föld kerületére 252000 stadion adódott. Egy kis bizonytalanság ennél az értéknél azonban fennáll, mivel a görögök kétféle stadiont használtak. De még így is a kapott érték alig 20%-kal nagyobb a mai nagy pontosságú adatnál, ha az egyik hivatalos stadiont, s 1%-on belül van, ha a másik hivatalos stadiont használjuk.

E primitívségükben is csodálatos eredmények csaknem ezer éven át kiestek az érdeklõdés fénykörébõl. A legközelebbi állomás ugyanis i. sz. 827-bõl való. Ekkor a történelem egy másik mozgékony és eszes népe, az arabok kísérelték meg a Föld sugarának megmérését. Õk csaknem 2°-os szögeltéréshez tartozó ívhosszat mértek meg Bagdadtól északnyugatra a Szindzsáv sivatagban, s az ívhossz méréséhez mérõléceket használtak. Pontosságukat sajnos éppen azért nem tudjuk megbecsülni, mivel a mérõlécek hosszúságának átszámítási léptékét nem ismerjük.

Közben kialakul és teljes uralomra jut Európában a középkor szemlélete. A Föld gömb alakúságának még a gondolata is tiltott. Csak 1525-ben méri meg ismét az ívhosszat J. Fernel francia orvos Amiens és Párizs között, kocsikerekeinek fordulatszámát és kerületét használva fel a méréshez. Egy évszázaddal késõbb belépnek a geodéziai módszerek. 1617-ben Snellius bevezeti a háromszögelési eljárást, s ezzel megkezdõdik a Föld pontosabb geometriájának a tudománya, a geodézia. Ezután gyorsan követik egymást az események, s a mérések arra kezdenek utalni, hogy a Föld nem pontosan gömb alakú. Talán a sors iróniája, hogy az elsõ ilyen irányú kísérletek a valósággal éppen ellentétes eredményekre vezettek. A franciák fokméréseikbõl azt a következtetést vonták le, hogy a Föld forgási ellipszoid ugyan, de az ellipszis csúcsai a sarkoknál vannak. Az ellipszoid talán azért merült fel, mert ez a gömbhöz legközelebb álló s legegyszerûbben jellemezhetõ felület.

Ekkor bukkan fel s kér helyet a Föld alakjának a problémájában a tömegvonzás.

A tömegvonzás és a súly kérdése ilyen vagy amolyan alakban már a fizika megszületésétõl fogva foglalkoztatta a kutatókat. Galileit még csak az erõ és mozgás kapcsolatai érdekelték, s szabadesési kísérletei az elsõ tapogatózó lépések a gravitációs mérések terén. Nála merült fel elõször, ha igen kis pontossággal is, hogy a tömegvonzás független a testek minõségétõl. Ez elsõ megfogalmazása volt a gravitáló és tehetetlen tömeg arányosságát kimondó elvnek, amelynek nagy pontosságú igazolása adott alkalmat Eötvös számára, hogy nevét beírja a fizika történetébe.

A tömegvonzással kapcsolatos tudatos mérések azóta számíthatók, amióta Newton a tömegvonzás törvényét kimondotta. A tömegvonzás kezdettõl fogva két nagy problémakörben játszott fontos szerepet: egyrészt az égitestek mozgásának, másrészt a Föld alakjának a kérdésében. Ma a két független probléma a mesterséges holdak révén szoros kapcsolatba került egymással.

A Földdel kapcsolatos elsõ alapvetõ gravitációs mérés mintegy 15 évvel elõzte meg Newton híres mûvét, a Philosophiae naturalis principia mathematicát. Ezt az alapvetõ gravitációs megfigyelést J. Richter párizsi csillagász végezte, aki csillagászati ingaóráját 1672-ben Párizsból Cayennebe vitte, ahol azt tapasztalta, hogy az tetemes késéssel kezdett el járni felállítása után. Miután megigazította, s visszatért Párizsba, a Cayenneben helyesen járó inga Párizsban ugyanannyit sietett, mint amennyit Cayenne-ben Párizshoz képest késett. A francia tudósok ezt a forgó Földön fellépõ nagyobb centrifugális erõre vezették vissza, azonban Newton és Huygens azon a nézeten voltak, hogy csupán a centrifugális erõ megnövekedése nem elegendõ a késés magyarázatára; szükséges azt is feltételezni, hogy a Föld a sarkokon lapultabb, mint az egyenlítõn. Ez az ingaóra megfigyelés irányította rá a kutatók figyelmét arra, hogy milyen döntõ szerepet játszik a Föld alakjának vizsgálatában a tömegvonzás.

A Newton-féle tömegvonzási törvény többféle mérési feladat elé állította a fizikusokat. Az elsõ feladat az volt, hogy valóban igazolják a tömegvonzás tényét bármely két test között. Igazolni kellett a tömegvonzásnak távolsággal fordított arányos voltát. Meg kellett határozni a tömegvonzási állandó értékét, bebizonyítani annak univerzális állandó voltát, tehát az anyagtól való függetlenségét.

A tömegvonzási törvény lehetõséget ad a tömeg mérõszámának a meghatározására. De a tömeg mérõszámát az erõhatással szemben kifejtett tehetetlenségével adta meg a newtoni mechanika. Annak érdekében, hogy a kétféle tömeg fogalmát megértsük, képzeljünk el egy vízszintes és egyenes vasúti sínt egy rajta elhelyezett vasúti kocsival. Adott mozdony ezt a vasúti kocsit állandó tolóerõ kifejtésével pl. 20 másodperc alatt gyorsítja fel 60 km/óra sebességre. Egy másik vasúti kocsi tömege akkor egyenlõ az elsõ kocsi tömegével, ha a mozdony hasonló erõkifejtéssel ugyancsak 20 másodperc alatt gyorsítja fel 60 km/óra sebességre. Míg a két kocsi együtt való felgyorsítására kétszer akkora erõt kell a mozdonynak kifejtenie, akkor is, ha a két kocsit nem a földön levõ sínpáron gyorsítják fel, hanem pl. a Holdon vagy a Jupiteren, ahol pedig mindkét kocsi súlya lényegesen kisebb, ill. lényegesen nagyobb. A tömeget tehát azzal a mérõszámmal lehet jellemezni, amely megmondja, hogy egységnyi gyorsuláshoz mekkora erõt kell a testre kifejtenünk. Ha nincs erõhatás, a test képtelen megváltoztatni sebességét, nincs gyorsulás. A tömeget tehát a tehetetlenségi állapotának megváltoztatásához szükséges erõvel mérik. Ezért ezt a tömegmérõszámot tehetetlen tömegnek nevezik. Két test tömegét össze lehet úgy is hasonlítani, hogy a súlyúk (tehát a Föld vonzása és forgása következtében kialakult erõ) nagyságát mérjük meg. A súly alapján is lehet tehát a tömeghez mérõszámot rendelni. Ezt gravitáló vagy súlyos tömegnek nevezik. Nem magától értetõdõ, hogy pl. egy aranyból készült vasúti kocsi és egy alumíniumból készült vasúti kocsi, amelynek tehetetlen tömegérõl megállapítottuk, hogy azonos, ugyanakkora súlyt is képvisel, tehát egy jól kalibrált mérlegen ugyanazt a mérõszámot mutatja. Igen kívánatosnak látszik bebizonyítani, hogy a kétféle mérõszám azonos.

A gravitációs törvény nagy pontosságú érvényességét elõször a bolygómozgás gravitációra alapozott elméletének a megfigyelésekkel való igen nagy pontosságú egyezése támasztotta alá. A tömegvonzásra vonatkozó elsõ kísérleti méréseket Cavendish hajtotta végre 1798-ban. Cavendish a tömegvonzás földi testeken való fellépésének kimutatása mellett a gravitációs állandó értékét is megmérte, s ebbõl megállapította a Föld átlagos sûrûségét. A Richter-féle megfigyelések ráirányították a figyelmet arra a szoros kapcsolatra, ami a nehézségi erõ és a Föld alakja között fennáll. Ezért a perui expedíció során, amelyet a Föld lapultságának meghatározása érdekében küldött ki a francia akadémia 1735-ben, Bouguer és la Condamine a geodéziai fokmérést már gondos ingamérésekkel egészítette ki. Itt merültek fel az ingalengés idejének meghatározására szolgáló módszerek csírái is, amit azonban tudatosan csak Borda dolgozott ki késõbb, a 19. század elsõ felében.

A 19. század elsõ feléig azonban a gravitációs mérések csak tapogatózások voltak, s kiegészítették a Föld alakjára vonatkozó elméleti eredményeket és geodéziai méréseket. Pontosságuk messze elmaradt attól, amit a Föld alakjának szabatosabb vizsgálata megkívánt volna.

A Föld alakjának modern értelemben vett fizikai és geometriai vizsgálata a XIX. század közepe táján indult meg, s csupán napjainkban, a mesterséges holdak segítségével jutott el kifogástalan megoldáshoz. A földalak kérdésének modern vizsgálata tehát Eötvös életében a tudomány egyik legizgalmasabb s legtöbb rejtélyt jelentõ problémája volt, s mindenkor a mérési pontosság legvégsõ lehetõségeinek a kihasználását kívánta. Nem csodálhatjuk, ha ez a kérdés a becsvággyal fûtött s klasszikus gondolkodású Eötvöst megfogta.

A Föld tényleges alakja igen változatos. Elméletileg azonban szükségünk van egy olyan felületre, amely a Földhöz jól rögzíthetõ, s amelyhez képest a tényleges földfelszín, a morfológia leírható. Az elméleti meggondolások éppúgy, mint azok gyakorlati megvalósítása arra vezetett, hogy a Föld alakját a nehézségi erõteréhez kössük. És itt néhány szót kell szólnunk a tömegvonzás és a nehézségi erõ közötti különbségrõl. A tömegvonzás törvényét Newton fogalmazta meg. Eszerint két pontszerû tömeg között olyan vonzóerõ lép fel, amely a tömegek mérõszámával arányos, de fordítva arányos a közöttük levõ távolság négyzetével. A Föld hatalmas tömege is összetehetõ pontszerû, tehát pl. a távolság méretéhez képest elhanyagolható nagyságrendû tömegrészecskék összességébõl, s így a Föld is egy adott pontszerû (vagy legalábbis igen kicsiny kiterjedésû) tömegre olyan vonzóerõt gyakorol, ami megfelel az egyes tömegrészecskék vonzásának erõösszegével, azaz vektor eredõjével. Azt is tudjuk, hogy homogén, tehát azonos sûrûségû övekbõl felépített gömb alakú test vonzása ugyanakkora, mintha az egész tömege a középpontjában lenne sûrítve, tehát pontszerûvé válnék. Valóban a Föld vonzása elsõ közelítésben akkora, mintha egész tömege tömegközéppontjában volna sûrítve.

De a Föld az égitesteknek közel tehetetlenségi koordinátarendszeréhez képest tengelykörüli forgást végez. Ezt a forgást magán a Földön, a Földhöz rögzített koordinátarendszerben úgy észleljük, mintha a tömegvonzáshoz egy másik erõ, mégpedig egy tehetetlenségi erõ, a Föld forgása következtében fellépõ centrifugális erõ adódnék hozzá. A vonzásnak és a centrifugális erõnek az eredõjét nevezzük a Földön nehézségi erõnek.

Hogyan köthetõ a Föld alakja a nehézségi erõtérhez? A Föld felszínének nagy részét tengerfelszín alkotja. A tengerfelszín, ha nem volnának tengeráramlások és légmozgások, olyan szintfelületet alkotna, amely mindenütt merõleges volna a nehézségi erõre. Ezt az elméleti tengerfelszínt libella segítségével, az ún. szintezõmûszer felhasználásával a szárazföld minden pontjára is kiterjeszthetjük. Így az egész Földre egy, az átlagos tengerszintjével azonos magasságban fekvõ szintfelületet kapunk, amelyet kizárólag a nehézségi erõ határoz meg, s amelyet földalaknak vagy geoidnak nevezünk. A régi vizsgálatok is rájöttek, hogy a szintfelülethez igen jól hozzáilleszthetõ egy forgási ellipszoid. Ez az ellipszoid azonban alig tér el a gömbtõl. Hogy az eltérést szemléletesen láthassuk, képzeljük el az egész Földet (s így a felszínét megközelítõ ellipszoidot is) a 20 milliomod részére kicsinyítve, ami azt jelenti, hogy a Föld sugarának nagyságrendje 30 cm körül lesz. Ha a lekicsinyített modellt a földtengelyen keresztülmenõ síkkal metsszük, s ellipszis helyett körzõvel egy olyan kört rajzolunk meg, amelynek nyomvonala 1 mm széles, akkor a megközelítõ ellipszishez (de magához a földfelszin lekicsinyített keresztmetszetéhez is) húzható úgy egy kör, hogy a lekicsinyített ellipszis, ill. tényleges keresztmetszet teljesen az 1 mm-es nyomvonalon belül marad. Ez azt jelenti, hogy a Föld tényleges alakja alig tér el a gömbtõl.

A pontosabb geodéziai és gravitációs vizsgálatok azonban azt is feltárták, hogy a tényleges földalak eltér az ellipszoidtól, bármennyire is jól közelíti azt meg. A tényleges földalaknak azonban kiemelkedései és süllyedékei vannak az ellipszoidhoz képest. A geoid felszíne tehát hullámzik, undulál. A geoidundulációk azonban, amint azt már ma a mesterséges holdakból levont igen nagy pontosságú eredményekbõl pontosan tudjuk, nem nagyobbak 50 m-nél, azaz alig lépik túl a szintfelületet helyettesítõ ellipszoid, tehát a Föld méreteinek az ezred százalékát.

E nagyobb kiterjedésû undulációkon kívül azonban a geoid kisebb, finomabb változásai mindenütt fellépnek. Az illedékekben fellépõ sûrûségkülönbségek éppúgy eltorzítják, mint ahogy eltorzítják a mélyben eltemetett tömegek is. Világos, hogy ezek hatása, ha létezik is, elképzelhetetlenül kicsiny. Eötvös egyik alapvetõ eredménye az volt, hogy megtalálta a mûszert és a módszert arra, hogy a földalaknak ezeket a kicsiny, egy pohár víz felszínén is észlelhetõ hullámzásait is meg tudja mérni. Az eszköz a módosított és rendkívül érzékennyé és megbízhatóvá tett Coulomb-inga volt, amelyet éppen ezért joggal nevezhetünk Eötvös-ingának (vagy Eötvös mérlegnek, ha az egyensúlyi helyzetek alapján való használatát vesszük figyelembe).

Milyen is az Eötvös inga szerkezete, s mivel érte el Eötvös az addig szinte ismeretlen nagyfokú pontosságot. Képzeljünk el egy vízszintes alumínium rudat, amely közepén egy vékony, befogott rugalmas szálhoz van rögzítve úgy, hogy felfüggesztés után is vízszintes marad. Világos, hogy ez a rúd egyensúlyba kerül, ha a szál ki van csavarodva; s ha ebbõl az egyensúlyi helyzetbõl a vízszintes irányba kimozdítjuk, akkor a szál igyekszik ugyanoda visszacsavarodni. Az egyensúlyt lényegesen nem zavarja, ha a vízszintes rúd két végére a forgástengelytõl ugyanakkora távolságra két egyenlõ aranytömeget (vagy más tömeget) teszünk, még akkor sem, ha az egyik tömeget külön szálon alsóbb szintre helyezzük. Ezzel elvileg el is készítettük az Eötvös-ingát. Az is világos, hogy ha a rudat tartó szál helyett vékonyabbat helyeznek el, akkor kisebb erõ hozhat létre ugyanolyan kitérést. Eötvös 0,02 mm átmérõjû platina, majd platina-iridium szálat használt, amelyet elõre kikészített erre a célra úgy, hogy ne legyenek benne felhalmozott feszültségek, hõérzéketlen legyen, s keresztmetszete mindenütt ugyanakkora s tartsa az egyensúlyi helyzetét. De ha ezt igen kicsiny erõk el tudják téríteni, akkor a mikroklíma következtében elõálló mikrolégáramlások állandóan változtatják majd a rúd helyzetét. Ezt kiküszöbölendõ Eötvös az ingáját kettõs, majd hármas falú, jól záró edénybe zárta, s észlelései alatt még külsõ sátorral is igyekezett az egyenetlen hõhatásokat kiküszöbölni.

Világos, hogy a teljes nehézségi erõ nem okoz semmiféle elcsavarást, ha az mindenütt állandó, mert nem lesz vízszintes összetevõ, ami a tömegeket s velük együtt a rudat elcsavarná. De ha a felszín alatt egy nagyobb sûrûségû tömeg van, akkor ez a tömeg az Eötvös-inga rúdjának két végén levõ súly közül a mélyebben, tehát közelebb levõ tömeget jobban vonzza, mint a kissé magasabban fekvõ másikat. Ez a két erõkülönbség elegendõ arra, hogy az ingát elcsavarja. Ez a csavaró hatás akkor érvényesül, ha nem pontosan a nagyobb sûrûségû tömeg felett vagyunk, hanem oldalról közeledünk feléje, azaz ahol a nehézségi erõ értéke növekedésben van. Az Eötvös-inga elcsavarodása tehát azokat a helyeket jelzi, ahol a nehézségi erõ értéke meghatározott irányban nõ, s az elcsavarodás ennek a növekedésnek a mértéke. A geofizikusok azt a mennyiséget, amely megadja azt, hogy a nehézségi erõ a vízszintes síkban egy cm-en belül mennyit nõ a legnagyobb növekedés irányában, a nehézségi erõ (nívófelületi) gradiensének nevezik. Az Eötvös-inga a térben elsõsorban a nehézségi erõ vízszintes gradiensét adja meg. Ezt a gradienst térképen egy olyan vektorral szokás feltüntetni, amelynek hossza a gradiens mértékét, és iránya a legnagyobb növekedés irányát jelzi. A gravitációs gyorsulás egységét, amely egy cm-es egységnyi sebességnövekedést jelez, Galilei tiszteletére 1 gal-nak nevezik. A nehézségi erõ nagyságrendje a Földön 1000 galhoz van közel, mégpedig a világ gravitációs alappontján, Potsdamban a pontos érték: 181,274 gal. A nehézségi erõ változása a szintfelületben rendkívül kicsiny. Elvileg ezt a változást gal/cm-ben kellene mérni, a gyakorlat azonban azt kívánta, hogy alkalmas egységül ennek a milliárdomod részét használjuk, azaz a gradiensnek 10^-9 gal/cm a geofizikában használt egysége. Ezt az egységet eötvös-nek nevezik.

Talán az elõbbiekbõl nem elég világos, hogy hogyan is kapcsolódik Eötvös gravitációs mérlege a Föld alakjához, és milyen módon is került Eötvös a geoid finom változásainak a méréséhez.

Az elõbbiekben vázoltuk, hogy a földalak vagy geoid megfelel a nehézségi erõ, egy az átlagos tengerszinttel összeesõ nívófelületével, s ez közelítõleg helyettesíthetõ egy forgási ellipszoiddal. A forgási ellipszoid adatait azonban ki lehet számítani a nehézségi erõ ismert értékei segítségével. Ezért a múlt század végén hatalmas kampányt indítottak el abból a célból, hogy a nehézségi gyorsulás értékét a Föld különbözõ pontjain meghatározzák. Magyarországon a Természettudományi Társulat vette ezt a kérdést elõször kezébe, s 1881-ben megbízta Eötvöst, hogy határozza meg a nehézségi gyorsulás értékét Budapesten, az Alföldön és a Kárpátokban. Eötvös, aki semmit sem tudott máskép végrehajtani, csak alaposan, e feladattal kapcsolatban arra törekedett, hogy a gravitáció természetét teljes mélységében feltárja, talán elõször saját maga elõtt, s a mérést minél nagyobb pontossággal végezze el.

Vizsgálatai elvezettek a csavarási mérleghez, s ezzel nemcsak a nehézségi erõ nagy távolságokra esõ változásait volt képes meghatározni, hanem annak a legfinomabb szintváltozásait is, hiszen az Eötvös-inga a vízszintesben 1 cm-en fellépõ olyan kis változást meg tud határozni, amely a teljes súly mintegy billiomod részének felel meg, tehát tényleg képes egy pohár víz felszínének gravitációból adódó alakját megadni. S ha ismerjük ezt a változást elég sok pontban, akkor két távoli pont között is meg lehet adni a nehézségi gyorsulást, jelezvén mindenütt a finomabb hullámzásokat is.

Ha egy adott területen a (nívófelületbeli) gradiensek területi eloszlását Eötvös-ingával megmértük, ez a területen a nehézségi erõ helyi legmagasabb és legalacsonyabb értékeit is kijelöli. A gravitációs értékek helyi maximumai körül a gradiensek mind a terület felé fognak mutatni, a depressziók helye körül pedig a depresszióktól kifelé irányulnak. Miután két gradiens közötti változást, ha ezek elég közel esnek egymástól, lineárisnak lehet feltételezni, ezért egy kiinduló érték ismerete esetén a nehézségi gyorsulás értéke (vagy annak az elméleti értéktõl való eltérése) a gradiensekbõl a terület minden pontjában kiszámítható. Megvan annak is a lehetõsége, hogy a nehézségi erõ eloszlását szemléletesen mutassuk be. Ezt úgy érhetjük el, hogy az azonos nehézségi gyorsulással bíró helyeket összekötjük. Miután ezekben a nehézségi rendellenesség értékét gal-okban (vagy milligal-okban, esetleg annak tört részében) adják meg, ezeket a vonalakat izogaloknak (néha izogammáknak) nevezik s a térképet izogal térképnek. Az izogal térképek a szintvonalas térképek hatását keltik, rendszerint azonban simábbak, szelídebbek azoknál. Miután ezek a térképek a felszínalatti tömegek sûrûségeloszlása szerint alakulnak ki, s a sûrûség általában ott növekszik meg, ahol a mélyebben levõ nagyobb sûrûségû tömegek megemelkedtek, ezért a térképek a mélybeli tömegek domborzati viszonyait fogják imitálni, de lesimítottan. Persze vannak ez alól kivételek is. Ilyen kivételt jelentenek a sótömzsök, amelyek mélybõl nyomulnak be a felsõbb rétegekbe, és a felettük levõ rétegeket is megemelik, azonban miután a kõsónak a sûrûsége kisebb a környezõ kõzetekénél, a sódómok felett gravitációs völgy, gravitációs depresszió van, jóllehet a rétegek megemelkedése áll fenn.

Miért érdekesek ezek az adatok azonkívül, hogy a tudományos megismerés számára a Föld arculatának a fejlõdését tárják fel elõttünk?

Az üledékekkel borított területek szerkezeti felépítése szoros kapcsolatot mutat a területen esetlegesen elõforduló kõolaj- és gázfelhalmozódásokkal, amelyek a mai technikai civilizáció számára egyelõre nélkülözhetetlen szénhidrogének forrásai. A kõolaj- és gázelõfordulások legtöbbször ott találhatók, ahol a rétegek megemelkedtek, azaz az úgynevezett antiklinálisokban. Érdekes, hogy az antiklinális elmélet alig néhány évvel az elsõ tudatos olajfúrás, azaz 1859 után merült fel, alkalmazása azonban csak a 19. század utolsó éveiben vagy még inkább a 20. század elején vált uralkodóvá. Az elmélet fizikai alapjai a kõolaj keletkezéssel vannak szoros kapcsolatban. A kõolaj keletkezésére kétféle elmélet van: az egyik elmélet szerves eredetre vezeti vissza a kõolajat, a másik szervetlenre. Mindkét elméletnek tekintélyes hívei vannak. Valószínûnek látszik, hogy a szerves eredetû kõolaj teszi ki a Föld tartalékainak tekintélyes részét. A szerves eredet gondolata vázlatosan a következõ: a tengerrel borított területeken egy folyamatos üledéklerakódás van folyamatban. Az üledékek azonban nemcsak a szervetlen alapanyagokból állanak, hanem a tengerben élõ nagymennyiségû algák, diatomák, meg nem emésztett állati anyagok keverékébõl, s a tengerfenéken kialakul elõször egy szervetlen iszapszerû anyag. Ezt helyenként és idõnként, különösképpen a partközeli területeken, ahol az üledékképzõdés mértéke a legnagyobb, a geológiai és morfológiai viszonyok megváltozásával együtt járó üledékösszetétel változás követi, ami lerakódott rétegek szemcseváltozásában nyilvánulhat meg. A rétegek, amelyek szerves anyagot is tartalmazhatnak, tehát szendvicsszerûen váltakozó homok- és agyagrétegekbõl állnak, ahol a homokréteg - porozitása miatt - a folyékony és gáz alakú alkatrészeket átereszti, az agyagos réteg pedig ezek számára szigetelõként lép fel. Természetesen a rétegek eloszlása a valóságban a most leegyszerûsített képnek szinte megszámlálhatatlan variációit rejti magában.

A vastag rétegek alá került iszapot alkotó szerves eredetû anyagok a nyomás és a hõmérséklet következtében, de egyéb katalizátorok következtében is felhasadnak, s egyszerûbb szénhidrogének egész sorozata keletkezhet, a metántól a parafinig vagy aszfaltig. Természetesen ebben az eredeti állapotban a szénhidrogéneknek a rétegben való koncentrációja olyan kicsiny, hogy az termelésre egyáltalán nem alkalmas. Ha azonban a Föld arculatát alakító erõk következtében úgynevezett tektonikai mozgások lépnek fel, akkor az eredetileg az ülepedésnek megfelelõen vízszintesen lerakódott rétegek helyenként felboltozódnak, s a porózus rétegekbe bejutott folyékony és gázhalmazállapotú szénhidrogének, valamint a víz fajsúly szerint igyekeznek migrálni, s a könnyebb alkatrészek a magasabb felé vándorolnak, migrálnak, a hidrosztatikus egyensúlynak megfelelõen. Ez lehetõvé teszi, hogy a víz és kõolaj szétváljék, s a szénhidrogének pl. a felboltozódás területére, általában pedig olyan kõolaj csapdákban koncentrálódjanak, ahonnan már továbbvándorolni nem tudnak. Ez elsõ közelítésben úgy is megfogalmazható, hogy az elsõdleges kõolajcsapdák éppen az antiklinálisok, a felboltozódások. Ez pedig éppen az antiklinális elmélet lényege.

Ha végiggondoljuk az Eötvös-inga elvét, világossá válik, hogy alkalmas antiklinálisok helyének felderítésére. Érdekes módon a tudományos köztudatban az van, hogy Eötvös nem látta ingájának ilyen irányú jelentõségét, s az Eötvös-inga olajkutatásra való alkalmazását Böckh Hugónak, a kiváló magyar geológusnak tulajdonítják, holott Eötvös pontosan tudatában volt mûszerének ilyen irányú jelentõségével is, legfeljebb annak ilyen értelmû aprópénzre váltását nem tûzte ki feladatának.

A gyakorlati alkalmazások lehetõségérõl hadd idézzük magát Eötvöst:

"Ismételten feltették nekem a kérdést, vajon lehet-e megfigyelési módszereimnek gyakorlati hasznát is venni. Nem lehetne-e segítségükkel elásott vagy tengerfenékre süllyedt kincsek helyét megtalálni, vajon forrásokat, érc-, szén- és sótelepeket nem lehetne-e felfedezni? Nem akar-e a tudomány a torziós mérlegével egy igen régi mûszert, a varázsvesszõt kiszorítani, amely sok évszázados hírnevét a hitnek köszöni? Nem, ezt nem akarjuk, ma bizonyosan nem, amikor még épp hogy csak az elsõ tapogatózó lépéseket tettük meg. Rejtett tömegeloszlások megismerését elõmozdító, rendszeresen folytatott munkával azonban lassanként kétségkívül közelebb jutunk ahhoz a lehetõséghez is, hogy a tömegek összességébõl a gyakorlatilag értékesebbet le tudjuk majd választani.

Azt, hogy egyes esetekben már a torziós mérleg egymaga is gyakorlati értékû útmutatással szolgálhat, hadd világítsuk meg a következõ példán.

A hasznosítható energia új forrásainak serény kutatása a legújabb idõkben több gyakorlati szakember érdeklõdését felkeltette az éghetõ földgáz iránt is. Magyarországon pl. az Alföldön egyes furatokból kiáramló gázok már több mint két évtizede világítási célokra és motorok üzemeltetésére alkalmazást nyertek. A legutóbb három év alatt azonban, az erdélyi igen gazdag gázforrások feltárása következtében, az ilyen gázok elõfordulásának kérdése rendkívüli gazdasági érdekességû problémává nõtt. Egyetlen, ott Kis-Sármás mellett feltárt 302 méter mély furat másodpercenként 10,55 m³, vagyis 24 óra leforgása alatt körülbelül egymillió köbméter, kémiailag csaknem tiszta metángázt szolgáltat.

Hol kell mármost ilyen gázok érdekében fúrni? A geológusok - úgy látszik - megegyeznek abban, hogy a gázt tartalmazó területen a legkiadósabb fúrások a gázokat vezetõ és azokat befedõ rétegek antiklinálisai (gerincei) közvetlen közelében sikerülnek. Emellett szólnak az Amerikában (Ohióban) szerzett tapasztalatok és a magában Erdélyben tett megfigyelések is, amennyiben a rétegek elhelyezkedését és eltolódását geológiai kutatások során fel lehetett tárni.

De az ilyen geológiai ismertetõjelek teljesen hiányoznak a nagy magyar síkság, az Alföld homokkal és humusszal fedett felületén. Aki tehát ott és hasonló területeken gázokat vezetõ antiklinálisokat keres, nem teheti meg, hogy tanácsot ne kérjen a torziós mérleggel végzett megfigyelésektõl. Hogy milyen sikerrel, azt a jövõ fogja megmondani."

Talán érdekes megemlíteni, hogy a zalai olajmezõt, amely az elsõ gazdaságos és jelentõs olajmezõje volt Magyarországnak, a torziós inga segítségével találták meg. A zalai területre az elsõ világháború után 1919-ben terelõdött a figyelem. A kutatás eredményességéhez a jugoszláv területen levõ peklenicai (Bányavár) olajmezõ közelsége adta a reményt. A kutatás geológiai munkával indult. Sajnos míg a Bányavár területén az antiklinálist a felszínen végzett geológiai mérésekbõl is jól ki lehetett jelölni, addig a zalai (budafapusztai) területen az már oly mélyre került, hogy a felszínen egyáltalán nem volt követhetõ, s a földtani térkép semmit sem mondott. Mégis 1923-ban a geológiai felvételekre, az abból levezetett dõlésekre telepítették az elsõ kutató fúrást, mégpedig kereken másfél kilométerrel a szerkezet tetejétõl délre. A fúrás 1737,5 métert harántolt át, de eredménytelen volt, s csupán fúrás közben észleltek gáz- és olajnyomokat, mivel a fúrás már termelõ területen kívül esett. Az eredménytelenség kereken tíz esztendõ késést okozott a mezõ felfedezésében. Az 1933-ban felújított kutatás már elsõsorban geofizikai, mégpedig torziós inga mérésekkel indult meg, de párhuzamosan földtani újratérképezés is folyt. A földtani kutatás bebizonyította, hogy ezen a területen a fiatal korú (pliocén) rétegek enyhén gyûrtek, de a földtani felvételezés adatai nem alkalmasak arra, hogy segítségükkel az antiklinális tengelye kijelölhetõ legyen. A torziós inga szempontjából sem volt nagyon kedvezõ a terep, mert a torziós ingát zavaró terepegyenetlenségek a méréseket eléggé zavarják, s így elsõsorban a kiszélesedõ völgyekre korlátozódtak. De ez is elég volt arra, hogy az antiklinális tengelyét kijelöljék. E terület torziós inga méréseit 1934-ben végezték. Fúrásra azonban csak 1936 nyarán került sor, és a következõ év márciusában fejezték be eredményesen. Azt lehet mondani, hogy a dunántúli olajmezõk nagyobbik részét a torziós ingának köszönhetjük. Talán történelmileg érdekes, hogy a torziós ingának olajkutatásban való alkalmazására akkor került sor Magyarországon, amikor a világon már megjárta diadalútját, s új mûszerek kezdték átvenni a szerepét a gyakorlati kutatásban. Hiszen az elsõ sikeres alkalmazása Texasban több mint tíz évvel megelõzte a magyarországi alkalmazást.

Az, hogy Eötvös nem tekintette feladatának a torziós inga gyakorlati alkalmazását, pontosan azt jelentette, hogy fõ feladatának az alapvetõ tudományos problémák megoldását s új módszerek kidolgozását tûzte maga elé. A gravitációs vizsgálatokban a torziós inga elsõ alkalmazása a fizika egyik alapvetõ problémájával kapcsolatban merült fel: ez a gravitáló és tehetetlen tömeg arányosságának a kérdése volt. Elsõ ilyen irányú munkája is ezzel foglalkozik, s utolsó (posztumusz) megjelent mûvének is ugyanez a célja, csupán a pontosságban van két nagyságrend különbség.

Azt hisszük, hogy e kérdés megvilágításánál leghelyesebben akkor járunk el, ha Eötvösnek azokat a szavait idézzük, amikor elõször beszél e problémáról. 1890. január 20-án a Magyar Tudományos Akadémián tartott, "A Föld vonzása különbözõ anyagokra" címû elõadásában a következõket mondja:

"Azon tételek között, amelyekre Newton az õ gravitációs elméletét alapította, a legfontosabbak egyike az, hogy a vonzás, amelyet a földi testekre gyakorol, tömegükkel arányos és anyagi minõségüktõl független. Már Newton kísérletekkel igazolta ez állítását. Nem elégedett meg a már elõtte ismert iskolai kísérlettel, amely azt mutatta, hogy üres térben a pehely és a pénzdarab egyformán esnek, felhasználta e célra a pontosabban észlelhetõ ingamozgásokat is. Ingákat szerkesztett, amelyekben egyenlõ nehézségû, de különbözõ anyagú testek: arany, ezüst, ólom, üveg, homok, konyhasó, víz, búza és fa lehetõleg egyenlõ sugarú köríveken mozogtak, s e lengési idõket megfigyelve, nem bírt közöttük különbséget megállapítani.

Newtonnak e kísérletei kétségtelenül sokkal pontosabbak a fent említett iskolai kísérletnél; pontosságuk mégis alig haladja meg az egy ezredet, úgyhogy szigorúan véve csak annyit bizonyítanak, hogy az ingáiban használt anyagok nehézségi gyorsulásai között egy ezredrészöknél nincs nagyobb különbség. A pontosságnak ez a foka nem tekinthetõ kielégítõnek ily fontos kérdés eldöntésére, s ez okból Bessel 1830-ban klasszikus ingakísérleteinek folyamában szükségesnek tartotta az újabb vizsgálatot. Méréseivel, amelyeket arany, ezüst, ólom, vas, cink, sárgaréz, márvány, agyag, kvarc és meteoritok lengéseire vonatkozólag tett, kétségtelenül megmutatta, hogy ezen anyagok nehézségi gyorsulásai között nem lehet nagyobb eltérés, mint e gyorsulásnak egy ötvenezred része. De nem elég még ez sem; jól mondja Bessel, hogy mindig érdekes lesz e tétel igazságát oly pontossággal megvizsgálni, amilyenre a haladó kor tökéletesedõ segédeszközei képesíteni fognak.

Különösen két okból kívánatos e vizsgálat. Elõször azért, mert Newton tétele veti meg az alapot, hogy a testek tömegét nehézségük által a mérlegen lemérhessük, s így a logika megkívánja, hogy az alaptétel helyes volta legalább a pontosság azon határáig bebizonyított legyen, amelyet a mérlegelésben elérhetünk; ez pedig az egy ötvenezredet messze túlhaladja, sõt az egymilliomodot is felülmúlja. Másodszor azért, mert Newton és Bessel kísérletei csak olyan testekre vonatkoznak, amelyek egymástól anyaguk eloszlását illetõleg aránylag kevéssé különböznek, s majdnem teljesen függõben hagyják a kérdést a sokkal ritkább légnemû testekre vonatkozólag. Bessel kísérleteibõl legfeljebb annyit következtethetünk, hogy a levegõre gyakorolt vonzóerõ nem különbözik többel a szilárd testekre vonatkozótól, mint egy ötvenedrésszel.

A tömegvonzásra vonatkozó vizsgálódások folyamában az én figyelmem is ráirányult e kérdésre, és amennyiben megoldása felé más úton haladtam, mint Newton és Bessel, és sokkal nagyobb pontosságot értem el, mint õk, érdemesnek tartom okoskodásom menetét és kísérleteim eredményét a t. Akadémiának elõterjeszteni.

Az az erõ, amelynek következtében a testek üres térben a Földre esnek, s amelyet nehézségnek nevezünk, két összetevõ erõnek, ti. a Föld vonzóerejének és a Föld forgásából származó középfutó erõnek eredõje. Ez a két összetevõ erõ általában nem egyazon és nem is ellentett irányú, hanem egymással szöget alkot, amely közel egyenlõ a geográfiai szélesség pótszögével. Az eredõnek iránya ez összetevõktõl függ; világos tehát, hogy a Földnek ugyanazon helyén, egyenlõ tömegû testek középfutó erõi egyenlõk lévén, e testek nehézségeinek különbözõ irányúnak kell lenniök, ha a rájuk gyakorolt vonzóerõk különbözõk volnának.

A nehézség irányában netán mutatkozó ilyen kicsi eltérések felismerésére a függõón és a libella (szintezõ) nem eléggé érzékeny eszközök. Jól használható azonban a csavarodási mérleg, úgy amint azt a nehézség irányában mutatkozó kicsiny eltérések felismerésére más vizsgálatoknál is már használtam.

Csavarodási mérlegeinkben a vékony platinadrótra akasztott 25-50 cm hosszú mérlegrúd végeire különbözõ, egyenként kb. 300 gr súlyú testeket erõsítettem. A rudat a meridiánra függõlegesen állítván, állását egy vele mozgó és egy másik, az eszköz szekrényéhez erõsített tükör segítségével pontosan meghatároztam. Aztán az eszközt szekrényestõl 180 fokkal elforgattam úgy, hogy az a test, amely elõbb a rúd keleti oldalán volt, most a nyugati oldalra jutott és viszont, s újból meghatároztam a rúd állását az eszközhöz. Ha a két oldalon alkalmazott testek nehézségei különbözõ irányúak volnának, a rudat tartó drót csavarodásának kellene bekövetkeznie. Ilyen azonban nem mutatkozott akkor, ha az egyik oldalon állandóan alkalmazott sárgaréz golyóval együtt, a másik oldalon üveg, parafa vagy antimonitkristályok voltak felfüggesztve; pedig a nehézség irányában 1/60000 másodpercnyi eltérésnek már az elsõ percnyi, biztosan észlelhetõ csavarodást kellett volna létesítenie.

Bátran állíthatok annyit, hogy ha egyáltalában van különbség a különbözõ anyagú, de egyenlõ tömegû testek nehézségei között, úgy ez a különbség sárgaréz, üveg, antimonit és parafára vonatkozólag egy húszmilliomodnál, sárgaréz és levegõre vonatkozólag pedig egy százezrednél bizonyára kisebb."

E munka s elvi jelentõsége csak másfél évtized múlva érett meg a nemzetközi tudományos köztudatban, s ennek jeleként a gravitáló és tehetetlen tömeg arányosságának nagy pontosságú bizonyítására pályázat kiírására került sor.

A problémát 1906-ban tûzte ki a göttingai tudós társaság, s Eötvös munkáját, amely az "Ars longa vita brevis" jeligét viselte, s az egyetlen pályázat volt, 1909-ben a Beneke alapítvány díjával tüntették ki. Eötvös a tehetetlen és gravitáló tömeg arányosságát már 1/200000000 pontossággal bizonyította torziós ingája segítségével. A tehetetlenségével mért és a tömegvonzásból mért tömeg arányossága alapját képezte az általános relativitáselméletnek. Jóllehet ennek fennállását Einstein elmélete kidolgozásakor feltételezte, Eötvös eredményei biztosították hozzá a kísérleti alapot. A mérés pontosságát lényegesen csak a legutóbbi idõben múlta felül Dicke, a princetoni egyetem tanára, felhasználva a modern mérési technika összes lehetõségeit.

Eötvös azonban a teljes gravitáció területét óhajtotta tisztázni. Így egy módszert dolgozott ki, s meghatározta nagy pontossággal a gravitációs állandó értékét. E mérésre új módszert dolgozott ki, amit éppen az jellemzett, hogy a mérési bizonytalanságokat a minimumra redukálta. E módszer abból állott, hogy a torziós inga lengésidejét mérte két párhuzamos ólomtéglafal között, mégpedig elõször úgy, hogy az inga rúdja a falakkal párhuzamosan, másodszor pedig azokra merõlegesen lengett. A két lengésidõbõl a gravitációs állandó G végtelen falak esetén így fejezhetõ ki:

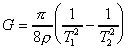
ahol T₁ és T₂ a két lengésidõ, mí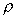g a fal anyagának sûrûsége. Ha a fal véges, akkor ehhez még egy korrekciós faktor szükséges, amely csupán a fal geometriájától függ.

A gravitációs állandó problémája ma túlnõtte azt az egyszerû szerepét, hogy egy alapjelenség mértékszámához szolgáltatja az arányossági tényezõ pontos értékét. A gravitációs állandó és az általános relativitás igen érdekes módon összekapcsolódik, s a modern geofizika és kozmológia egyik fontos tényezõjévé vált.

Dirac 1938-ban ugyanis arra a meggondolásra jutott, hogy a gravitációs állandó a valóságban egy idõparaméter függvénye. Az idõparaméter nagyságrendileg a Naprendszer korával azonos nagyságrendû, s a gravitációs állandó ezzel a paraméterrel fordítottan arányos.

Dirac gondolata a maga idejében nem keltett túlzott érdeklõdést egy-két fanatikus hívétõl (Jordan P., Milne E. A.) eltekintve, azonban a kozmológiának és geofizikának az utolsó évtizedben történt óriási fejlõdése és kiszélesedése következtében ismét az érdeklõdés elõterébe került, s ma már egy sorozat jelenség teszi valószínûvé Dirac félig bizonyított sejtését. A mai mesterséges holdak módszerei és a legutóbb, a Holdra elhelyezett laser-tükör valószínûleg néhány éven belül lehetõvé teszik ennek a kérdésnek eldöntését. Hogy itt e kérdéssel kapcsolatban egyebet ne említsünk, a gravitációs állandó csökkenése megoldást ad a Naprendszer keletkezésének kérdésében fennálló eddigi ellentmondások kiküszöbölésére; elméleti alapját szolgáltatja a földtágulási elméletnek stb. Az elv alkalmazása eddig is egy sorozat olyan jelenségre adott kézenfekvõ magyarázatot, amelyeket eddig körmönfont és erõszakolt feltevésekkel tudtak csak a kutatók értelmezni.

A gravitációs kutatások terén Eötvösnek még egy inkább metodikai kísérleti, mint elvi jelentõségû eredménye volt, amelyet mégis úgy szoktak emlegetni, mint Eötvös-hatás. Ez pedig az volt, hogy kísérletileg megmutatta, hogy a nyugatról keletre mozgó testek könnyebbek, mint a keletrõl-nyugatra mozgók. Ez elvileg világos, hiszen az ilyen mozgó testek nehézségi ereje nagyobb, ill. kisebb centrifugális erõ eredõjeként áll elõ, mint a Földhöz képest álló testek esetében. A jelentõsége mégis abban volt, hogy az idõ tájt kezdõdtek meg a nagyobb pontosságú gravitációs mérések a tengeren, s a hatás már felülmúlta a mérés pontosságát, aminek következtében e tengeri mérések adatai nagyobb szórást mutattak a vártnál.

Eötvös ennek a hatásnak a mérésére és kimutatására a következõ módszert dolgozta ki: forgó zsámolyra szerelt fel egy mérleget. Ha a forgó zsámolyt forgatta, a mérleg egyik súlya váltakozva kelet-nyugat felé, a másik nyugat-kelet felé mozgott. A fellépõ hatás következtében a két tömeg között súlykülönbség lépett fel, s az eredeti egyensúly felbomlott, azaz ha elegendõ idõ állt volna eme állapot fenntartására, a mérleg karja az eredeti vízszintesbõl elmozdult volna. Azonban a hatás is kicsiny s az állapot ideje is rövid volt. Ezért Eötvös szellemes fogással a rezonancia elméletét használta fel a jelenség kimutatására. A mérleg egy lengõ rendszer, amelynek megvan a saját lengésideje. Ha a forgó zsámolyt olyan sebességgel forgatjuk, hogy a mérleg megfelelõ súlya abban a helyzetben csökkenjen, amikor éppen felfelé való lengésben van és viszont, akkor fellép egy rezonancia s a kicsiny hatásokat fel lehet annyira erõsíteni, hogy az jól észlelhetõvé váljék. Sõt. Eötvös egy egyszerû módszerrel, mégpedig a mérlegkarokra elhelyezett mágnessel és egy mesterséges mágneses térrel ezt a hatást kiegyensúlyozta (a karok lengését kiküszöbölte), s ezáltal a fellépõ erõhatást meg tudta mérni. A mért hatás nagy pontossággal megegyezett az elméletileg levezetett értékkel.

A gravitációs és a mágneses térnek sok tekintetben hasonló szerkezete arra vezette Eötvöst, hogy a mágneses tér mérésével is foglalkozzék. A mágneses tér vizsgálatához is az Eötvös-ingához hasonló mûszert szerkesztett. Ezt a mûszert õ mágneses translatométernek nevezte. A mágneses erõtér változását 5 független mennyiség jellemzi. Ebbõl négyet a translatométerrel lehet meghatározni. A mágneses tér azonban sokkal erõsebben változik, mint a gravitációs tér, sõt az idõbeli változásai is nagyok. Ezért Eötvös mûszere túl érzékeny is volt a tér változásainak mérésére. Talán még Eötvös maga is túlbecsülte a méreteket, amikor 1896-ban a következõket írja: "Eszközeim nem arra valók, hogy velük egy ország vagy világrész általános mágneses térképét vegyük fel, hanem inkább arra, hogy azokat a változásokat keressük fel, amelyeket a mágneses erõben közelfekvõ tömegek, hegyek, völgyek vagy a Föld belsejében elrejtett mágneses kõzetek létesítenek. Ily értelemben jó szolgálatot tehetnek a geológiának."

Mágneses mûszerei még ennél sokkal finomabb változások mérésére voltak alkalmasak. Itt mi néhány szót szeretnénk szólni Eötvösnek azokról az úttörõ méréseirõl, amelyeket az archeomágneses kutatások terén végzett, s amelyek méréséhez a translatométert használta fel.

Talán kissé általánosabban a paleo- és archeomágneses mérések lehetõségérõl kell néhány szót szólnunk. Az anyagok jó részének megvan az a tulajdonsága, hogy mágneses térben mágnesessé válhatnak. E mágnesesség két részbõl áll: egy állandó részbõl, amelyet remanens mágnesezettségnek nevezhetünk, s amely a test kémiai felépítéséhez és geometriájához van kötve, amíg annak megváltoztatására drasztikus külsõ hatás nem kényszeríti; másrészt egy átmeneti részbõl, amelyet indukált mágnesezettségnek nevezünk, s amely a mindenkori mágneses tér irányát követi.

Minden test elveszti azonban remanens mágnesezettségét egy bizonyos hõmérsékleti érték felett. Ezt a hõmérsékletet Curie-féle pontnak szokás nevezni.

A magmás kõzetek keletkezésénél a hõmérséklet rendszerint messze a Curie-pont felett van, tehát nincs remanens jellegû mágnesezettség bennük. Ha azonban a Curie pont alá hûlnek, akkor a jelenlevõ mágneses tér hatására magukba fagyasztják e térnek az irányát, azaz maguk a meglevõ tér irányának megfelelõen mágnesezõdnek, s azt megtartják. Késõbb ehhez a mágnesezettséghez a tér változásával újabb és újabb irányok járulhatnak hozzá, s a kõzet, amely talán sok millió évvel ezelõtt keletkezett, e hatások összességét hordozza magában, s ma ezt észlelhetjük. A késõbbi mágneses hatások a kõzetek egy tekintélyes részénél olyanok, hogy azok könnyen eltávolíthatók. Azaz, a kõzet a keletkezése után rárakódott hatásoktól megtisztítható, s a keletkezésekor fennálló mágneses erõtér iránya és néha nagysága is ebbõl meghatározható.

Mindezek együttvéve lehetõvé teszik, hogy az egykori mágneses tér szerkezetét a Föld pólusainak egykori helyzetét a mai kontinensekhez képest meghatározzuk, s ezzel fizikailag is alátámasszuk a geológusoknak azokat a feltevéseit, amelyeket õk a sokkal bizonytalanabb s pontatlanabb földtani megfigyelések alapján vezettek le. Az utóbbi negyedszázadban kialakult tehát a paleomágnesség tudománya, amely pontos leírást tudott adni arról, hogy a Föld sarkai hogyan vándoroltak a földtörténet folyamán, sõt lehetõvé tette azt is, hogy a kontinensek vándorlásának a hipotézisét is fizikailag bizonyíthassuk. (A kontinensvándorlás elmélete azt mondja, hogy valamikor az összes kontinens egyetlen összefüggõ területet alkotott, majd ez az egységes kontinens, a pangea szétszakadt, s az egyes kontinensek eltávolodtak egymástól, s kerültek végre a mai helyzetükbe. Ezért esik egybe annyira pontosan Dél-Amerika keleti és Afrika nyugati partvonala.)

A régi mágneses tér iránya nemcsak a kõzetekben rögzítõdhet, de rögzítõdhet agyagkancsókban vagy téglákban azok kiégetésekor, s így a történeti vagy történelem elõtti korok mágneses terének az irányát meg lehet ebbõl határozni. Ez a tudományterület az archeomágnesség.

Eötvös mágneses translatométerének kipróbálásával a paleomágneses vagy még pontosabban az archeomágneses kutatások egyik korai elõfutárává vált, mert egy sorozat ismert korú korsóból megállapította az akkori korok mágneses terének irányát. Adatai jól belevágnak a más módszerekkel meghatározott egykori mágneses térirányokba.

Hátrahagytuk azt a területet, amely Eötvös nevét elõször alapozta meg, s amely területre soha nem tért vissza a gravitációs vizsgálatai elkezdése után. Ez volt a kapillaritás jelensége. E jelenségekre elõször egyetemi hallgató korában lett figyelmes königsbergi tanulmányai alatt. Akkor dolgozta ki azt a módszert, amelyet csaknem 20 évvel késõbb alapvetõ eredményeinek eléréséhez használt fel. E módszert F. Neumann szemináriumában ismertette. Dicséretet is kapott érte, de csak 1876-ban közölte a rövid életû Mûegyetemi Lapok-ban.

A folyadék felszínét alkotó hajszálcsövesség vagy kapillaritás szoros összefüggésben áll a folyadékmolekulák energiaviszonyaival. Eötvös bevezette a molekuláris felületi energia fogalmát, amelyet úgy definiált, mint azt a munkát, amelyet ahhoz kell végezni, hogy a folyadékfelületet akkora felületdarabbal növeljük, mint amekkorát átlagosan egy molekula borít. (Talán ez a szemléletes, bár nem precíz definíció felmenti e sorok íróját attól, hogy a pontosan körülírt, de sok fogalmat kívánó definíciót megadja.)

Eötvös elméleti meggondolásokra alapított hosszadalmas kísérletsorozat alapján kimutatta, hogy a felületi energia változása az ún. "egyszerû folyadékok" esetében arányos a hõmérsékletváltozással, s az arányossági tényezõ ugyanúgy univerzális állandó, akárcsak az általános gáztörvény esetében. A két formula is hasonló, csupán a nyomás szerepét az egységnyi molekuláris felülethez tartozó munka, a térfogatot a molekuláris felület, tehát a moltérfogat 2/3 hatványa, az abszolút hõmérséklet szerepét pedig a kritikus hõmérséklettõl való eltérés veszi át. A gázállandó helyett ebben az összefüggésben egy kapilláris állandó szerepel, amelynek értékét Eötvös 0,227-ben állapította meg. Ma is a fizikai irodalomban ez a törvény Eötvös-törvényként szerepel.

Ha Eötvös fizikai és geofizikai vizsgálatait figyelemmel kísérjük, akkor a következõ mindenkor és minden kutató által követésre méltó elveket emelhetjük ki:

1. Az elmélet és a kísérleti igazolás együttessége.

2. A mérések pontosságának a végsõkig való fokozása.

3. Az összes befolyásoló tényezõk figyelembevétele és a mérési pontosság alá szorítása.

4. A laboratóriumi eredmények és a gyakorlati élet kapcsolatának tisztázása.

Jóllehet, Eötvös az utóbbi princípiumot sohasem használta ki a saját hasznára és elõnyére, munkássága a mi életünknek nemcsak szellemi, de anyagi fellendülését is elõsegítette.

																EGYED LÁSZLÓ

A rezgések intenzitása, tekintettel a rezgési forrásnak és az észlelõnek mozgására. Budapest 1874. Magyar Tudományos Akadémia. 23. 1. (Értekezések a mathematikai tudományok körébõl III.)

Über die Intensität der wahrgenommenen Schwingungen bei Bewegung der Schwingungsquelle und der Beobachters. Pogg. Annalen der Physik 1874. 513-535.

Új módszer a capillaritási tünemények tanulmányozására. Mûegyetemi Lapok 1876. 2-10.

A távolbahatás kérdésérõl. A Magyar Tudományos Akadémia Évkönyvei XVI. 1877. 57-68.

A folyadékok felületi feszültségeinek összefüggése a kritikai hõmérséklettel. Mathematikai és Természettudományi Értesítõ 1884. 54-73.

Über den Zusammenhang der Oberflächenspannung der Flüssigkeiten mit ihrem Molekularvolumen. Annalen der Physik und Chemie 1886. 448-459.

Untersuchungen über Gravitation und Erdmagnetismus. Annalen der Physik und Chemie 1896. 354-400.

Vizsgálatok a gravitáció és a mágnesség körébõl. Mathematikai és Physikai Lapok 1896. 22-26.

Jedlik Ányos emlékezete. Akadémiai Értesítõ 1897. 273-289.

A nehézség és a mágneses erõ nívófelületeinek és változásainak meghatározása. Mathematikai és Physikai Lapok 1900. 361-385.

A föld alakjának kérdése. Természettudományi Közlöny 1901. 321-328.

Programme des recherches gravimétriques dans les régions vésuviennes. Comptes rendus des séances de la premiére réunion de la commission permanente de l'Association International de Sismologie réuni á Rome. 177-179.

Bestimmung der Gradienten der Schwerkraft und ihrer Niveauflächen mit Hilfe der Drehwage. Leiden 1907. Brile. 59. 1., 1. t. (Klny. az Abhandlungen der 15. Allgemeinen Konferenz der Erdmessung in Budapest 1906. c. mûbõl.)

Sur les travaux géodétique exécutés en Hongrie, spécialentent á l'aide de la balance de torsion. Budapest 1909. Imp. Hornyánszky. 40. 1 térkép.

Experimenteller Nachweis der Schwereiänderung die ein auf normal geformter Erdoberfläche in östlicher oder westlicher Richtung bewegter Körper durch diese Bewegung erleidet. Annalen der Physik 1919. 743-752.

Beiträge zum Gesetze der Proportionalität von Trägheit und Gravität. (Pekár Dezsõvel és Fekete Jenõvel.) Annalen der Physik 1922. 11-66.

Gesammelte Arbeiten. Hrsg. (und Vorwort) von P(ál) Selényi. Budapest 1953. Akadémiai Kiadó, Akadémiai ny. LXXX, 384. 1., 45.

Báró Eötvös Loránd élete és tudományos mûködése. Írták: FEKETE JENÕ, MIKOLA SÁNDOR stb. Bp. 1918. Franklin. - (2) 113-295. (1) 1., 1 t. (Klny. a Mathematikai és Physikai Lapokból.)

B. Eötvös Loránd Emlékkönyv. Szerk.: FRÖHLICH IZIDOR. Az MTA kiadása Bp. 1930.

PETRU BOGDAN: Bemerkung über die Berechnugsweise der Kapillaritätskonstanten. Die Regel von Eötvös-Ramsay. Der Kompressibilitätskoeffizient der Flüssigkeiten. Zeitschr. f. phys. Chem. 82. 1913. 93.

M. BORN u. R. COURANT: Zur Theorie des Eötvösschen Gesetzes. Phys. Zeitschr. XIV. 1913. 731.

E. MADELUNG: Kinetische Theorie des Gesetzes von Eötvös. Phys. Zeitschr. XIV. 1913. 729.

MAURICE PRUD'HOMME: Quelques conséquences de la loi d'Eötvös-Ramsay. Journ. chim. phys. 14. 1961. 285-290.

A. P. METHEWS: The relation of molecular cohesion to surface tension and gravitation; with a method of determining "a" of Van der Waals' equation without assumption; and the explanation of the meaning of the constants in the surface tension law of Eötvös and the latent heat formulas of Dieterici and Mills. Journ. phys. chem. 20. 1961. 554-596.

MITSURU SATO: On the Kinetic Theory of Eötvös Law in Sutface Tension. Sc. Reports Tohoku Univ. XV. 1926. 805-817.

O. EGGERT: Theorie und Anwendung der Drehwage von Eötvös. Zeitschrift f. Vermessungswesen 42. 1. 1913. 474-483. és 505-517.

DESIDER PEKÁR: Die geophysikalischen Messungen des Baron Roland v. Eötvös. Die Naturwissenschaften VII. 1919. 149-159.

R. L. STEINER: The Eötvös law concerning the connection between the local disturbances of the magnetic force and those of gravity. Terrestrial Magnetism and Atmospheric Electricity XXVI. Baltimore 1921. 81-90.

H. SHAW AND E. LANCASTER-JONES: The Eötvös Torsion Balance. Proceedings of the Physical Society of London. 35. 1. 1923. 151-166. (irodalmi összeállítással).

H. SHAW AND E. LANCASTER-JONES: Application of the Eötvös Torsion Balance to the investigation of Local Gravitational Field. Proc. of the Phys. Society of London 35. 1. 1923. 204-212.

P. NIKIFOROV: Sur le variométre de gravité d'Eötvös. Acad. d. Sc. Russie. C. R. d. Seances d. la Comm. sismique permanente. Tome VII. 3. 1924. 343-381.

PEKÁR DEZSÕ ÉS FEKETE JENÕ: A gravitáció és tehetetlenség arányosságáról. Math. és Phys. Lapok XXVII. 1918. 188-205.

ALBERT EINSTEIN: Autobiographical Notes. P. A. Schlipp: Albert Einstein Philospher-Scientist. Tudor, New York 1949. 65.

R. H. DICKE: Principle of Equivalence and the Weak Interactions. Review of Modern Physics. XXIX. 1957. 355-362.

EGYED LÁSZLÓ: A gravitációs mérések fejlõdése. Fizikai Szemle XI. 1959. 291-295.

R. H. DICKE: Eötvös Experiment and the Gravitational Red Shift. American Journal of Physics XXVIII. 1960. 344-347.

R. H. DICKE: The Eötvös Experiment. Scientific American 205. 1961. 84-95.

RENNER JÁNOS: Megjegyzések az Eötvös-kísérletekrõl szóló cikkhez. Fizikai Szemle XII. 1962. 223-224.

EGYED LÁSZLÓ: Gravitáció, geofizika és csillagászat. Fizikai Szemle 1964. jan.

MARX GYÖRGY: Az Eötvös kísérlet mai szemmel. Fizikai Szemle 1966. 12. 372.

Eötvös home page