Kérdések Bolyai János kutatásairól

Kiss Elemér

S. E. olvasónktól kaptuk a következõ sorokat Különös érdeklõdéssel olvastam a Természet Világa ez évi augusztusi számában megjelent Foglalkozott-e számelmélettel Bolyai János? címû cikket Az írással kapcsolatban két kérdés merült fel bennem, amelyekre szeretnék bõvebb felvilágosítást kapni

1. Eddig úgy tudtuk, hogy Bolyai fõleg a geometria kérdéseivel foglalkozott. Hogy lehet az, hogy már egészen korán a számelmélettel is találkozott?
2. Szívesen olvasnék részletesebben a komplex számok aritmetikájáról s Bolyainak ezzel kapcsolatos eredményeirõl

A szerzõ válasza

1. Bolyai János valóban igen fiatalon megismerhette a számelmélet alapvetõ kérdéseit. Apja könyvtárában már 1804-ben ott volt Gaussnak Bolyai Farkas szerint "halhatatlan" Disquisitiones arithmeticae címû nevezetes könyve, amely tartalmazza kora számelméletének legfontosabb és legújabb problémáit. Gauss mûvét már 13 éves kora után olvashatta Bolyai s bizonyára olvasta is, ui. ekkor már tudott latinul. Farkas 1816. április 10-én írta Gaussnak: "... felnõtt tanítványaimmal együtt nyilvánosan igen dicséretesen vizsgázott deákul..." Hogy az 1820-as években milyen alaposan tanulmányozta Bolyai János a Disquisitiones-t, kitûnik apjának Gausshoz írt másik, 1831. június 30-án kelt levelébõl: "Fiamnak szándéka volt, hogy a Te polygon-elméletedet németül, a kisebb kaliberû elméknek valamivel könnyebben hozzáférhetõ módon adja ki..." Amint tudjuk, Gauss a polygon-elméletét a Disquisitiones arithmeticae-ben fejti ki.
De mindezeknél többet mond erre a kérdésre vonatkozóan Bolyai János saját nyilatkozata. A marosvásárhelyi Teleki-tékában õrzött kéziratos hagyaték 1214/2-es számozású lapján ceruzával írt német nyelvû szövegben ez áll: "Már kisgyermek koromban feltettem magamnak a kérdést, hogy végtelen sok prímszám létezik­e?" Ezek szerint Bolyai János tényleg egészen fiatalon találkozott a prímszámokkal és mindjárt megfogalmazta a velük kapcsolatos egyik legfontosabb kérdést is.
Arról, hogy Bolyai Jánosban igen korán jelentkezik a matematika iránti szenvedélyes érdeklõdés, eddig csak apjának Gausshoz intézett leveleibõl értesülhettünk. A fent említett följegyzésben viszont maga jelenti ki, hogy már gyermekkorában foglalkoztatta a számelmélet egyik legfontosabb kérdése. A kéziratokat lapozva még találkoztam Bolyainak egy ehhez hasonló vallomásával az 1389/1 oldalon is. Itt azt írja: "már elsõ fiatal, sõt gyermekkoromban magamtól is találtam, átláttam, rámentem", hogy

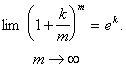
2. A komplex számok aritmetikáján a komplex számoknak oszthatósági szempontból való vizsgálatát értjük. Ha a, b racionális egészek, akkor az a+bi komplex számot komplex egésznek vagy Gauss­egésznek nevezzük. Az absztrakt algebra terminológiáját használva a Gauss­egészek a komplex számok összeadására és szorzására nézve kommutatív gyûrût alkotnak, akárcsak a racionális egészek az egész számok összeadására és szorzására nézve. A Gauss­egészek gyûrûjében is kiépíthetõ a racionális számelmélet analogonja, vagyis beszélhetünk az oszthatóság, a maradékos osztás, a legnagyobb közös osztó, a prímek stb. fogalmakról, éppen úgy, mint a racionális egészek gyûrûjében.

A komplex számok aritmetikájának kidolgozása Gauss nevéhez fûzõdik. Új prímszám­elmélet keletkezett ezzel, amelyben a 3, mint komplex egész is prímszám, de

A komplex egészeket oszthatósági szempontból Bolyai János is sokat vizsgálta. Õ is rájött arra, hogy ezek halmazában az oszthatóság alaptulajdonságai megmaradnak. Ez is egyike azoknak a kérdéseknek, amelyekrõl a Bolyai­irodalomban eddig még semmit sem olvashattunk. Jól ismert ugyan a Responsio címû munkája, amellyel Bolyai a komplex számok modern elméletének az egyik megalapozója, de a komplex számok oszthatóságával kapcsolatos eredményei még feldolgozásra várnak.

Gauss 1831­ben publikálta a komplex számokra vonatkozó munkáját. Nem tudjuk pontosan megmondani, hogy Bolyai János mikor dolgozta ki saját elméletét, de az biztos, hogy az 1830­as évek elején már õ is behatóan foglalkozott a komplex számokkal. Mivel Gauss munkája nyomtatásban is megjelent, míg Bolyai számításai csak kéziratos hagyatékának különbözõ lapjain õrzõdtek meg, így feladatunk csak annak a kérdésnek a megválaszolása lehet, hogy vajon Bolyai ismerte­e Gauss munkáját, vagy tõle függetlenül, önállóan dolgozott?

A rendelkezésünkre álló adatok azt igazolják, hogy Bolyai János egyedül érte el felfedezéseit. Az alábbiakban szeretném részletesebben megindokolni véleményemet. Több módon is megpróbálom ezt a föltevést alátámasztani.

Vegyük szemügyre elõször Bolyai Farkas és Gauss levelezését. A levelekben több alkalommal esik szó a komplex számokról is, s ha figyelmesen követjük a két jó barát írásait, azokból kiolvashatjuk, hogy Gauss elméletének fontosabb része nem jutott el Marosvásárhelyre.

Gauss annak idején két elõadásban ismertette elméletét. Elsõ elõadását 1831. április 15­én, a másodikat pedig egy héttel késõbb, április 23­án tartotta. Második elõadásának szövege megtalálható a Göttingische gelehrte Anzeigen 1831­es évfolyamának 625­638­as oldalain. Erre az írásra, a megjelenés pontos helyét is megjelölve, maga Gauss hívta fel Bolyai Farkas figyelmét a nevezetes 1832. március 6­án írt levelében: "...benne találod néhány oldalon kifejtve a képzetes mennyiségekre vonatkozó nézeteimet, ..., nem nehéz megszerezni, ..."

Feltûnõ, hogy a Göttingische gelehrte Anzeigen 1831­es évfolyamából hiányzik az elsõ elõadás szövege, pedig amint Gauss összes mûveinek II. kötetébõl megtudhatjuk, éppen ez az elõadás tartalmazza a komplex számok oszthatóságával kapcsolatos legfontosabb problémákat, így például a komplex prímek leírását is. A folyóirat 1831-es példánya még eljutott Marosvásárhelyre (ma is megvan a Teleki­tékában), de további számai nem érkeztek meg. Így Gauss 1831. április 23­án tartott elõadásának szövegét Bolyai János is ismerte. Jegyzeteiben több helyen hivatkozik rá, a Responsióban pedig még bíráló megjegyzéseket is fûz hozzá.

Érthetetlen, hogy Gauss miért nem értesítette Bolyai Farkast 1832­ben elsõ elõadásáról is, s arról a késõbbiekben sem írt. Gauss 1832. március 6­ai levelére Bolyai Farkas 1835. április 20­án válaszolt s az "imagináriusokról szóló közlést" akkor köszönte meg. Közben hírt kapott Gauss elsõ elõadásáról is, mert már a következõ, október 4­ei levelében ezt írta: "Szeretném tudni, hogy kijött­e a munkád az imgaináriusokról s hol szerezhetném meg, mert a hirdetés óta semmit sem tudok". Majd évekkel késõbb 1848. január 18­án így panaszkodott Gaussnak: "Hosszan vártam imaginárius­teoriád kifejtésére, és már felhagytam minden reménnyel. Csak néhány héttel ezelõtt olvastam egy kis magyarhoni munkában, hogy megjelent Müller Archiv der Mathematik I kötetének 4. füzetében, de semmi egyéb nem állt róla. "

Olvasva ezeket a sorokat elhihetjük, hogy Bolyai Jánosnak még 1848­ban sem lehetett tudomása Gauss munkájának fontosabbik részérõl s így valóban önállóan alkotta meg az általa "prímtan"­nak nevezett komplex aritmetikát.

Föltevésünket alátámasztják még Bolyai János saját nyilatkozatai is, amelyeket különbözõ kéziratlapokról gyûjthetünk össze. Már cikkünkben is idéztük: "A prímek kirekesztõ formulájának... sikerülnie kell, még pedig bármi idomúak legyenek." Nyilvánvaló utalás arra, hogy nemcsak a racionális egész prímek, hanem a komplex prímek képletének megtalálásában is reménykedik ekkor. Vagy: "... a prímek általam régóta az imagináriumokra is kiterjesztett elemi tulajdonságaiból..." Más helyen: "... az imagináriusokat is befoglalva, mirõl már Gauss megint még csak nem is szól. " Meggyõzõek a következõ sorok is, amelyeket 1850 után jegyzett le Bolyai: "Igaz, hogy én éppen ezekben a vizsgálatokban, mikor e tárggyal majdnem egy negyed századdal ezelõtt foglalkoztam reájutottam a képzeteseknek igaz elméletére és ezt bõvítettem, meg próbára tettem." Valóban próbára tette, hisz a komplex egészekkel kapcsolatos eredményei segítségével bizonyította be igen egyszerûen például Fermat karácsonyi tételét.

Legfõbb érvünk pedig az, hogy Bolyai János egyetlen följegyzésében sem említi Gauss munkáját (az 1831. április 15-ei elõadásra gondolunk). Õ, aki más alkalommal sohasem mulasztotta el, hogy az írásaiban felhasznált bármilyen már ismert tételnek forrását ne idézte volna. Jegyzeteiben sokszor hivatkozott Euler, Lagrange, Vega, Gauss, Bolyai Farkas és mások mûveire, pontosan megjelölve azokat az oldalszámokat vagy sokszor a paragrafusokat, amelyekben az általa alkalmazott eredmény megtalálható. Ha olvasta volna Gauss elõadásának szövegét, akkor följegyzéseiben biztosan idézte volna azt.

Kéziratos hagyatékának tanúsága szerint Bolyai János a komplex egészek kérdésein is sokat tépelõdött. Elméletébõl nem készített összefüggõ dolgozatot. Azt csak kéziratainak különbözõ lapjairól tudjuk összeállítani. Errõl egy most készülõ dolgozatban igyekszem beszámolni.

Most még csak azt szeretném bemutatni, hogy Bolyai milyen világosan megkülönbözteti egymástól a prímszámokat aszerint, hogy azokat mely számhalmazban vizsgálja. Így azokat a számokat, amelyek a racionális egészek gyûrûjében prímszámok (a "közönséges" prímszámok), tehát például a 2, 3, 5, 7... számokat fõszámoknak, azokat, amelyek csak a komplex egészek gyûrûjében prímek, mint például az 1+1, 1+2i, 2-3i, ... komplex egészek tökélyes prímeknek, s végül azokat a számokat, amelyek úgy a racionális egészek, mint a komplex egészek gyûrûjében is prímek, azaz például a 3, 7, 11, ... (a 4k+3 alakú prímszámok) számokat pedig abszolút prímeknek nevezte.

Természettudományi és tudománytörténeti dokumentumok