
"Bárcsak Gauss túlélõje lenne..."
"Utinam Gauss superstes esset!"
(Bolyai János levele apjához)
Foglalkozott-e számelmélettel
Bolyai János ?
Kiss Elemér
A számelmélet a matematika egyik
legrégibb és legérdekesebb ága. Elsõsorban
az 1, 2,-3 4, ... természetes számok tulajdonságait
kutatja. Ezek a legközelebbi számismerõseink,
egyben a legkiismerhetetlenebbek is. Ezért a számelmélet
valóságos tárháza az érdekes,
sokszínû, nemegyszer reménytelenül nehéz
problémáknak. Bár a számelméleti
tételek megfogalmazása igen gyakran rövid és
egyszerû, bizonyításuk sokszor hosszadalmas
és nehéz. Mégis az elmúlt évszázadok
folyamán sok kiváló matematikust vonzott
az ebben az elméletben található feladatok
szépsége és változatossága.
Vajon Bolyai János találkozott a számelmélet
érdekfeszítõ kérdéseivel? S
ha találkozott, hogyan fogadta azokat? Sikerült talán
az abszolút geometria megalkotójának ebben
a tudományágban is új eredményeket
felismernie? Az alábbiakban kéziratainak újabb
átvizsgálása alapján válaszolunk
ezekre a kérdésekre.
Azóta, hogy a múlt század végén megtörténtek az elsõ lépések a Bolyaiak hagyatékának feltárására és ápolására, úgyszólván megszakítás nélkül folyik a kutatás, újabb meg újabb eredményekkel gazdagítva a szakirodalmat. Az elmúlt évtizedek során rangos monográfiák (Paul Stäckel, [1] Dávid Lajos, [2] Alexits György, [3] Weszely Tibor [4]), tudományos dolgozatok, népszerûsítõ cikkek születtek, amelyek szerzõi sokoldalúan ismertetik Bolyai János (1802-1860) életét, munkásságát. Már-már azt hihetnénk, hogy nincsenek fehér foltok a Bolyaikra vonatkozó ismereteink térképén. A Bolyai Jánossal foglalkozó mûvek fõképpen geometriai vizsgálatait helyezik elõtérbe. Ez természetes, hisz õ geometriai felfedezéseivel írta be nevét a matematikatörténetbe.
A Bolyai János munkásságát méltató legtöbb munka megemlíti ugyan, hogy kísérletezett számelméleti problémák megoldásával is, de sietve hozzáteszik, hogy ezen a téren nem ért el semmilyen említésre méltó eredményt. Már az elsõ és mindmáig a legtartalmasabbnak ítélt Bolyai-monográfia szerzõje, Paul Stäckel könyvében (1913) több helyen beszámol arról, hogy milyen természetû számelméleti feladatok foglalkoztatták Bolyai Jánost. Megírja, hogy ezekre apja, Bolyai Farkas (1775-1856) buzdította õt már fiatal korában, de aztán hozzáteszi: "Elõrehaladott korában is foglalkozott számelmélettel, de kevés sikerrel, úgyhogy a tárgyra vonatkozó följegyzéseivel nem érdemes foglalkoznunk." Alexits György 1977-ben ezt írja: "Bolyairól tudjuk, hogy foglalkozott számelméleti kérdésekkel is, de ezekrõl csak egy-két, érthetetlen jelekkel teleírt cédula és levélboríték adhatna felvilágosítást, ha ki lehetne hámozni az odavetett jelek értelmét. De nem valószínû, hogy számelméleti kísérletei valamilyen értékes eredményt tartalmaznának..." Egyedül Weszely Tibor fogalmaz 1981-ben óvatosan, az igazságot jobban megközelítõen, amikor megjegyzi, hogy Bolyainak a számelmélet terén semmiféle jelentõsebb eredményérõl nincs tudomásunk. Ez valóban így is volt, amikor Weszely nagy sikerû könyve napvilágot látott.
Bolyai János kéziratos hagyatékának nagy részét Marosvásárhelyen, a Teleki-Bolyai Könyvtárban õrzik. A mintegy 13 000 oldalnyi kézirat legújabb áttanulmányozása eredményeképpen az eddig megjelent monográfiákban hangoztatott állításokat szükséges átértékelnünk, sõt helyreigazítanunk. A kézirathagyaték lapjai, az eddig még feltáratlan több Bolyai-levél arról tanúskodik, hogy a fenti véleményekkel ellentétben a geométer Bolyai János igen élénken érdeklõdött a számelméleti kérdések iránt. Õt is megejtették a "matematika királynõjének" nehéz feladatai, és amint látni fogjuk, olyan följegyzéseket is rejtegetnek a kéziratok, amelyeket kibetûzve meglepõdve fedezzük fel Bolyai Jánosnak a számelmélettel kapcsolatos gondolatait, amelyekkel megelõzte más matematikusok késõbb közzétett munkáit. Sajnos, ezek az eredmények máig ismeretlenek maradtak. Így történhetett meg például, hogy az egyik szép Bolyai-tétel ma nem Bolyai Jánosnak, hanem újrafelfedezõjének nevét viseli.
De ne siessünk túlságosan elõre...
Nézzük meg rendre, mindvégig a kéziratokat faggatva, hogy miképpen vélekedett Bolyai János a számelméletrõl, annak nagy alakjáról, Gaussról, remekmûvérõl, a Disquisitiones arithmeticae-rõl, majd pedig vizsgáljuk meg a hagyatékban eddig "rejtõzõ" néhány számelméleti eredményét.
Bolyai Jánost a számelmélet valósággal elbûvölte. Nyilatkozata errõl jó példája egyik sajátosságának, hogy sok följegyzésében egyes szavakhoz több rokon értelmû új szót tesz hozzá: "A számelméletben nemcsak az egész számok, hanem az egész tan legfontosabb, leghasznosabb, leglényegesebb, legszebb, legérdekesebb, legkecsesebb feladatait találjuk". Ismert, hogy C. F. Gauss (1777-1855) is igen kedvelte a számelméletet. Tõle származik a mondás, hogy ha a matematika a tudományok királya, akkor a számelmélet a matematika királynõje. Bolyai, bár nagy tisztelõje a "göttingai kolosszus"-nak, õt a számelmélet nagymesterének nevezi, mégsem ért ezzel egyet. "Gauss igen korán fõleg a számelmélettel foglalkozott - állítja. - Ez életfogytáig kedvenc tárgya maradt, amelyet, habár nem jogosan, a matematika királynõjének nevezett."
1801 nyarán látott napvilágot a számelmélet alapvetõ tankönyve, Gauss Disquisitiones arithmeticae címû munkája. Néha e könyv megjelenésétõl számítják a modern számelmélet kezdetét. A Disquisitiones Bolyai János kézikönyve volt, tehát jól ismerte, sokat forgatta. A számelmélet sok tételét ebbõl a könyvbõl olvasta. Ma ez a munka a Magyar Tudományos Akadémia könyvtárában található, benne Bolyai egyre halványuló széljegyzeteivel. De Farkasnak is volt egy példánya Gauss munkájából a szerzõ dedikációjával (Amico suo de Bolyai per curam Pauli Vada, auctor), amelyet aztán õ a Teleki-tékának ajándékozott (A Teleki Thecanak adom néhány egyébbel együtt, Bolyai Farkas).
Erre a mûvére Gauss is büszke volt. Egy 1808. szeptember 2-án Bolyai Farkashoz írt levelében úgy nyilatkozik, hogy a Disquisitiones arithmeticae-t csak hat matematikus értette meg egész Európában. Ugyanitt a számelméletrõl szólva azt mondja: "Figyelemre méltó, hogy bárkit, aki komolyan foglalkozik ezzel a tudománnyal, igaz szenvedély kerít hatalmába."
A Disquisitionest Bolyai János
sem tartotta könnyû olvasmánynak. Idézzük
két mondatát. Egyrészt "Az ki az emberi
elméknek egyik legremekebb és mélyebb mívén
erejét meg akarja próbálni, és magát
a netaláni maga - kétség - korságából
meggyógyítani, annak ajánlom például
a Göttingai kolosszus Gaussnak Disquisitiones arithmeticae
címû munkáját". Másrészt
"... a készülõ prímtannak bármely,
tehát a Disquisitiones arithmeticaenak is bármely
theorémáját procerto (bizonyosan - K. E.)
megmutathatni, problémáját resoválhatni
és így erre nézve, az egész Disquisitiones
arithmeticae-t zsebbe tehetni ugyan: noha másfelõl,
azon ABC-je az õ módjának, sajátságos
és sokkal nehezebb volta miatt mind az enyim mellett is,
örök-megtartást és nagyra becsülést,
respective bámulatot érdemel".
Bolyai János legtöbbet a prímszámokkal veszõdött. "Az egész számtan sõt az egész tan mezején - vallja - alig van szebb és érdekesebb... s a legnagyobb nyiászok (matematikusok - K E.) figyelme és eleje óta elfoglalt tárgy, mint a fõszámok (prímszámok - K. E.) oly mély homályban rejlõ titka".
Egy olyan eljárást keresett - mint olyan sokan mások -, amelynek segítségével bármely törzsszám megfelelõ képlettel kifejezhetõ. Egyidõben úgy érezte, hogy ezt a szándékát sikerül megvalósítania. Egyik följegyzésén így fogalmaz: "...nagyobbra nõtt, hágott azon régóta táplált sejtelmem és reményem, miszerint a fõszámokat hányadikságuk által függetlenül vagy egyenesen, közvetlenül is kitehetem, ... vagyis egy oly idomot (képletet -K. E.) adni, mely alatti számok mind fõk". Ugyanezt a gondolatot olvashatjuk ki apjának írt egyik igen bizakodó hangú levelébõl: "A prímek kirekesztõ formulájának is már nincs kételyem, hogy még pedig rövid idõn, sikerülnie kell, még pedig bármi idomúak legyenek. Utinam Gauss superstes esset! (Bárcsak Gauss túlélõje lenne! - K. E.). Erre és még sok más hasonlók eléggé legtekintélyesebb méltányolhatására nézve is".

"Bárcsak Gauss túlélõje lenne..."
Lehet közömbösen olvasni Bolyai János fájdalmas felkiáltását? Bárcsak Gauss túlélõje lenne! Ki ne érezné ebbõl a néhány szavas széljegyzetbõl azt a lelke mélyén rejtõzõ titkos vágyat, hogy bár Gauss is tudomást szerezne az õ felfedezéseirõl. Mennyire sóvárgott az elismerés akármilyen parányi sugaráért! S ezt egész életében leginkább Gausstól várta.
Köztudott, hogy Bolyai Farkas 1832 januárjában kéri Gauss véleményét az Apppendixrõl: "... - fiam többre becsüli az ítéletedet mint egész Európáét - és csakis erre vár." A választ is ismerjük. Aztán 1846-ban ismét azt tanácsolja apjának, hogy a képzetes mennyiségekkel kapcsolatos munkákról kérjék ki "más elismert... jó ízlésû tanászok ítéletét (például egy Gaussét)". De végül is sem õ, sem pedig apja nem fordult még egyszer Gausshoz, pedig Bolyai János Gauss halálát azért is gyászolja, "mivel az igazi jó mathematicumnak megítélésében rajtunk kívül legcompetensebb bíró veszett el a tan ... kárára".
Bolyai János a prímszámképletet elõször az ún. kis Fermat-tételben vélte felfedezni (P. Fermat 1601-1665). Ez a tétel azt mondja ki, hogy ha p prímszám, a pedig olyan egész szám, amely nem osztható p-vel, akkor az ap-1-1 különbség osztható p-vel, amit röviden a következõképpen szoktunk írni
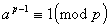 . (1)
. (1)
Például 212-1 = 4095 osztható 13-mal, 316-1 = 43 046 720 osztható 17-tel, de 211-1 = 2047 nem osztható 12-vel.
A kis Fermat-tétel fordítottja azonban nem érvényes, azaz ha igaz (1), vagyis ha az a p-1-1 különbség osztható p-vel, abból nem következik szükségszerûen, hogy p prímszám. Bármely a egész számhoz találhatunk olyan összetett p számokat is, amelyekre az (1) kongruencia fennáll.
Például 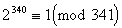 ,
bár
,
bár 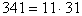 és
és
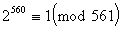 , de
, de
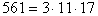 .
Az olyan összetett
p számokat, amelyekre az (1) kongruencia a=2 esetén
teljesül, álprímeknek nevezzük. Ezek szerint
341 és 561 álprímek. Vannak olyan p
összetett számok is, amelyek minden, p-hez
relatív prím a-ra kielégítik
a kis Fermat-tételt. Az ilyen p-ket felfedezõjükrõl
Carmichael-számoknak nevezzük. A matematikusok sokat
vizsgálták ezeket a különleges számokat.
Érdekes történetükben Bolyai János
is fontos szerepet játszott. Igaz, hogy ez a szerep ismeretlen
maradt a matematika történetében.
.
Az olyan összetett
p számokat, amelyekre az (1) kongruencia a=2 esetén
teljesül, álprímeknek nevezzük. Ezek szerint
341 és 561 álprímek. Vannak olyan p
összetett számok is, amelyek minden, p-hez
relatív prím a-ra kielégítik
a kis Fermat-tételt. Az ilyen p-ket felfedezõjükrõl
Carmichael-számoknak nevezzük. A matematikusok sokat
vizsgálták ezeket a különleges számokat.
Érdekes történetükben Bolyai János
is fontos szerepet játszott. Igaz, hogy ez a szerep ismeretlen
maradt a matematika történetében.
Apja ösztönzésére megpróbálta bebizonyítani a kis Fermat-tétel fordítottját. Néhány kísérlet után azonban rádöbbent arra, hogy ez lehetetlen, vagyis a kis Fermat-tétel fordítottja általában nem érvényes. Több olyan összetett számra, álprímre bukkant, amelyekre az (1) összefüggés fennáll.
A 341-es szám felfedezésérõl
így számol be apjának egy 1855 májusában
írt levelében: "A tegnapelõtt
ígért 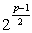 -re
nézve ugyan ezelõtti vizsgáimat
hirtelen nem kaphatván elé, vagyis inkább
akarván újból gondolkozni rajta, még
tegnap tisztába jöttem mire nézve itt rövidségért
bõvebb tárgyalást mellõzve a fõ
dolog iránti kétely és nyugtalanság
eloszlatására elég már a következõket
is közölni: ...mi pedig a legközelebbi és
tulajdonképpeni fõ kérdés, hogy éppen
-re
nézve ugyan ezelõtti vizsgáimat
hirtelen nem kaphatván elé, vagyis inkább
akarván újból gondolkozni rajta, még
tegnap tisztába jöttem mire nézve itt rövidségért
bõvebb tárgyalást mellõzve a fõ
dolog iránti kétely és nyugtalanság
eloszlatására elég már a következõket
is közölni: ...mi pedig a legközelebbi és
tulajdonképpeni fõ kérdés, hogy éppen
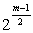 is lehet
is lehet 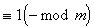 bár is m nem prím,
minek megmutatására persze elég egyetlen
példa is, mint a következõ, melyre ugyan csak
történetesen de még sem vaktában, hanem
elmélet után mentem.
2340-1 oszlik
(
bár is m nem prím,
minek megmutatására persze elég egyetlen
példa is, mint a következõ, melyre ugyan csak
történetesen de még sem vaktában, hanem
elmélet után mentem.
2340-1 oszlik
(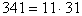 )-gyel...
úgy, hogy tehát sem a Fermat theoréma
sem a
)-gyel...
úgy, hogy tehát sem a Fermat theoréma
sem a 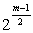 -re nézti szép sejtelem (mely ha a dolog természete
szerint valósulhatott volna, egy excellens és nagyon
kényelmes új isme-jele (critériuma) lesz
a prímeknek), nem csak, hogy generaliter nem, hanem még
azon különös esetben sem állanak, ha
a = 2...".
-re nézti szép sejtelem (mely ha a dolog természete
szerint valósulhatott volna, egy excellens és nagyon
kényelmes új isme-jele (critériuma) lesz
a prímeknek), nem csak, hogy generaliter nem, hanem még
azon különös esetben sem állanak, ha
a = 2...".

"A tegnapelõtt igért
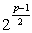 -re
nézve..."
-re
nézve..."
Talán megbocsátja a kedves olvasó,
ha itt egy személyes élménnyel tolakszom
elõ. A hagyaték lapozgatása során
elõször Bolyai János idézett levele
került a kezembe. A levél izgalmas matematikai tartalma
mellett különösen megragadott a következõ
két mondatfoszlány: "...ezelõtti vizsgáimat
hirtelen nem kaphatván elé, ..." és,
hogy eredményét "... nem vaktában, hanem
elmélet után..." találta. Vajon mi lehet
azokban a régi jegyzetekben? Léteznek-e még
valahol? Munkám talán legnagyobb jutalma az volt,
amikor néhány hét elteltével elõkerültek
a Bolyai által "hirtelen" nem talált jegyzetek.
Ezekbõl tudtam aztán kihámozni a fenti levélben
említett "elméletét". Bolyai János
itt azt vizsgálja, hogy az 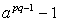 különbség
milyen feltételek mellett osztható a pq szorzattal,
ha p és q prímszámok, a
pedig egy olyan egész szám, amely nem osztható
sem p-vel, sem q-val. Arra a következtetésre
jut, hogy ez akkor teljesül, ha
különbség
milyen feltételek mellett osztható a pq szorzattal,
ha p és q prímszámok, a
pedig egy olyan egész szám, amely nem osztható
sem p-vel, sem q-val. Arra a következtetésre
jut, hogy ez akkor teljesül, ha
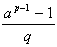 és
és
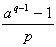
egész számok. Az a = 2
egyszerû esetben aztán rendre kipróbál
néhány, ezeket a feltételeket kielégítõ,
prímszámot s így eljut a p = 11
és q = 31 számokhoz, vagyis ahhoz
az eredményhez, amelyet a levelében is olvashatunk:
"2340-1 oszlik
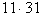 -gyel"
(részletes
bizonyítás az
[5]-ben
található)!
-gyel"
(részletes
bizonyítás az
[5]-ben
található)!
Bár Bolyai levelében kiemeli, hogy a Fermat-tétel fordítottjának megcáfolására "persze elég egyetlen példa is", mégsem elégszik meg a legkisebb álprímszám, a 341-es felfedezésével. Újabb és újabb példákat keres és talál. Így megszerkeszti a
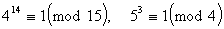 és a
és a

kongruenciákat is, amibõl arra következtethetünk, hogy ez a probléma sokat foglalkoztatta õt.
Hangsúlyozzuk: a matematika történetében
Bolyai János az elsõk között kérdõjelezi
meg a Fermattétel fordítottjának érvényességét.
Õ akkor szerkeszt több ellenpéldát is
erre a tételre, amikor a matematikai irodalomban csak elvétve
találunk ilyen természetû próbálkozásokat.
Bolyai persze ezekrõl nem tud. A számelmélet
történetét tárgyaló munkák
megemlítik, hogy a 341es számot egy ismeretlen
szerzõ már 1830-ban (tehát Bolyai elõtt)
megtalálta, F. Sarrus pedig 1820-ban felírta a
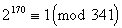 kongruenciát. E két cikk birtokában állíthatjuk,
hogy szerzõik más módon érték
el eredményeiket, mint Bolyai.
kongruenciát. E két cikk birtokában állíthatjuk,
hogy szerzõik más módon érték
el eredményeiket, mint Bolyai.
De ez az "elmélet" még más
meglepetéseket is tartogat. A különbözõ
tudományok történetei több olyan esetet
följegyeztek már, amikor kevésbé szerencsés
tudósok felfedezései életük folyamán
nem váltak ismertté, azokat csak kézirataik
õrizték meg, s majd hagyatékuk késõbbi
átvizsgálása hozta felszínre. Így
van ez Bolyai János számelméleti munkáival
is. Ha figyelmesen olvassuk el Bolyai módszerét,
amellyel példái egy részét megtalálta,
azonnal szembetûnik: ez a számelmélet egyik
jól ismert tétele, amelyet több mint 40 évvel
késõbb J. H. Jeans újból felfedez
és 1897-ben közöl nyomtatásban. Emiatt
ezt az elõször Bolyai által megtalált
nevezetes tételt ma Jeans-tétel néven ismerjük:
ha 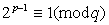 és
és
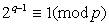 akkor
akkor
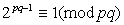 [6].
[6].
Érdemes összehasonlítani Bolyai bizonyítását Erdõs Pál egyik 1949-ben írt dolgozatával. Ennek egyik részében Erdõs Pál ugyanazt a gondolatmenetet követi, amelyet már Bolyai is alkalmazott vagy 100 évvel azelõtt.
Természetesen sem Jeans 1897-ben, sem Erdõs
1949-ben nem sejtette, hogy e gondolatokat valaki már rég
leírta s azok Marosvásárhelyen a Teleki-tékában
szunnyadnak.
Több szétszórt lapon, de néhány összefüggõ, hosszabb írásban és apjának írt leveleiben is foglalkozik Bolyai János azzal a tétellel, amely a 4k+1 alakú prímszámok két négyzet összegére való felbontásáról szól. A matematika története ezt a tételt is Fermat-nak tulajdonítja. Mivel Fermat felfedezését egy 1640. december 25-én kelt levelében közli M. Mersennenel (1588-1648), a tételt Fermat karácsonyi tételének is nevezik. Fermat ezt a tételt nemcsak megsejtette, hanem bizonyítására is felvázolt egy módszert. Teljes bizonyítást majd csak L. Euler (1707-1783) talált rá 1754 körül.
Fermat karácsonyi tétele: minden 4k+1 alakú prímszám a tagok sorrendjétõl eltekintve egyértelmûen felírható két egész szám négyzetének összegeként. Például
Bolyai Farkas a Teleki-tékában, ahol
"kedvesen lehet elálmodni az alig kiállható
kedvetlen életet", olvasta Euler fent említett
bizonyítását. Igen hosszúnak (55 olal!)
és bonyolultnak találta s ezért arra biztatta
fiát, hogy kísérelje meg annak egyszerûbb
igazolását. János megfogadta apja tanácsát,
s egy levélben, mindössze két oldalon, mindjárt
három bizonyítást küld neki. Ami ezek
rövidsége mellett leginkább lebilincselõ,
hogy Bolyai János bizonyításaiban a komplex
egészek (azok az a + ib alakú komplex
számok, ahol a és b egész számok)
tulajdonságait alkalmazza. Egyik bizonyításában
például a Disquisitiones arithmeticae-re hivatkozva
abból a tételbõl indul ki, amely szerint,
ha p egy 4k + 1 alakú prímszám,
akkor létezik olyan x egész szám,
hogy
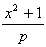 is egész szám.
Ezt
is egész szám.
Ezt 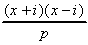 alakba írva már könnyedén kapja,
alakba írva már könnyedén kapja,
hogy p = a2 + b2 [7].
Érdemes itt is elidõzni azon, hogy mennyire újak, eredetiek Bolyai gondolatai. Nos, határozottan állíthatjuk, hogy Bolyai János nemcsak geometriai rendszerét, hanem számelméleti eredményeit is másoktól függetlenül, önállóan fedezte fel.

"Azt megmutatni,
hogy bármely 2p-1 idomú szám prím..."
Ennek igazolására igyekeztem több kollégám segítségével beszerezni mindazokat a múlt századi dolgozatokat, amelyek szerzõi a Bolyai által kutatott témákat tárgyalták, és azokat összehasonlítottam jegyzeteivel. A nyújtott segítséget ezúttal is köszönöm Gyõry Kálmánnak, Kalmár Istvánnak (Debrecen), Czapáry Endrének (Gyõr) és Lõrinczi Józsefnek (Groningen, Hollandia). Ez az összehasonlítás perdöntõnek bizonyult. Bár néhány írásban Bolyai gondolataival közõs ötletek is felvillannak, de a bizonyítások egészének vagy nagy részének a menete minden esetben különbözõ. Így például G. Eisenstein is a komplex egészek segítségével bizonyította be 1844-ben Fermat tételét, de a Bolyaiétól teljesen eltérõ módon. C. Hermite és J. A. Serret bizonyításaikban 1848-ban ugyanabból a tételbõl indulnak ki, akárcsak Bolyai, de a folytatásban már nem a komplex egészeket használják, hanem a lánctörteket hívják segítségül.
Bolyai magányosan, elszigetelten dolgozott.
Távol élt a matematikai tudományos élettõl,
nem jutottak el hozzá folyóiratok, nem ismerte mindig
kortársai felfedezéseit. Ezért fáradozott
hosszú éveken át a Ruffini-Abel-tétel
bizonyításával is
[8].
Különben az volt a szokása, hogy ha írásaiban
valahányszor már ismert tételt vagy más
ismert eredményt felhasznált, azoknak forrását
mindig feltünteti. Sokszor hivatkozik jegyzeteiben, az oldalszámokat
is megjelölve, Euler, Lagrange, Vega, Gauss, Bolyai Farkas
és mások mûveire.
Elhiszi a kedves olvasó, hogy Bolyai János bûvös négyzetet (ami olyan természetes számokkal képzett négyzetes mátrix, amelynek minden sorában, minden oszlopában és mindkét átlójában lévõ számok összege ugyanaz) is szerkesztett? Pedig így van. Egy nyugodt pillanatában elszórakozott a számokkal. "Lazított" õ is egyszer, de meglehet, hogy nagyon komolyan vette ezt a játékot is.
Úgy tûnik, hogy az a néhány sor, amelyet a bûvös négyzetet tartalmazó kézíratlapra írt Bolyai, csak a befejezését alkotja egyik gondolatának. Nem sikerült megtalálnom az írás feltételezett kezdetét.
| x | y | 3b-x-y |
| 4b-2x-y | b | 2x+y-2b |
| x+y-b | 2b-y | 2b-x |
Bolyai általánosan, betûkkel
szerkeszti meg bûvös négyzetét, amelybõl,
ha a betûk helyébe különbözõ
értékeket helyettesítünk, vigyázva
arra, hogy mindig természetes számokat kapjunk,
más-más, ún. szoros, hézagos vagy
ismétléses felépítésû
bûvös négyzetekhez jutunk.
A természetes számok körében Bolyai Jánosnak sem sikerült - nem sikerülhetett megtalálni a prímszámok képletét. Teljes eredménnyel járt viszont a komplex prímek leírása a komplex egészek gyûrûjében. Ismerte Gauss 1831-ben publikált értekezését, amelyben kifejti a komplex számok aritmetikáját, de õ a Gauss dolgozatában foglaltakat kiegészítette, új gondolatokkal bõvítette. Bolyai is kidolgozta ezek elméletét, amint írja "... a prímek általam régóta az imagináriumokra is kiterjesztett elemi tulajdonságaiból...". Félreérthetetlen utalás arra, hogy a komplex egészek elméletét is másoktól függetlenül, egyedül alkotta meg.
Különbözõ oldalakon pontosan
megmutatja, hogy melyek a komplex prímek. Itt csak megjegyezzük,
hogy azokat a számokat, amelyek az egész számok
és a komplex számok gyûrûjében
is (a 4k + 3 alakú prímszámok)
abszolút prímeknek, míg azokat amelyek csak
a komplex egészek gyûrûjében prímek,
tökélyes prímeknek nevezi.
Anélkül, hogy túlságosan belemerülnénk a részletekbe, a következõkben még megemlítünk néhányat azokból a számelméleti problémákból, amelyeket Bolyai János fölvetett.
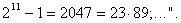
A számelmélet más kérdéseit is megtaláljuk a hagyaték lapjain, de úgy érzem, az elmondottak alapján is bátran felelhetünk "igen"-nel a címben feltett kérdésre, sõt ennél többet is mondhatunk. Bolyai János nemcsak foglalkozott a számelmélettel, hanem olyan eredményekkel gazdagította azt, amelyekre más matematikusok csak utána, évtizedek múlva gondoltak. Bolyainak ezek az írásai ellentmondanak annak az általánosan elterjedt véleménynek, amely szerint õ mindig mély geometriai szemléletére támaszkodott, eredményei és eredeti gondolatai is mindig geometriai tartalmúak. A cikkünkben tárgyaltak talán elég meggyõzõen mutatják, hogy Bolyai János nem kizárólag a geometriában alkotott nagyot. Kora matematikájának minden ága érdekelte, sokoldalú, eredeti tudós volt. Ha alkalma lett volna eredményeit különbözõ folyóiratokban vagy könyvekben publikálni, akkor ma a nevét nemcsak geometriai, de algebrai és számelméleti szakkönyvekben is gyakran megtalálhatnánk.

Bolyai János a számelmélet más területén is
probálkozott
Eddig úgy tudtuk, hogy a magyar matematika a múlt század utolsó negyedéig nem tud felmutatni említésre méltó számelméleti eredményeket. A fentiek és Bolyai Farkas néhány, eddig feldolgozatlan írása azt mutatják, hogy a magyarországi számelméleti kutatások kezdetét jóval elõbbre kell helyeznünk. Ezek valójában a két Bolyai tevékenységével kezdõdnek meg Magyarországon. A kéziratok tanúsága szerint Bolyai Farkast is érdekelték számelméleti kérdések. Nemcsak biztatta fiát különbözõ számelméleti feladatok megoldására, hanem õ is próbálkozott ezekkel, ha nem is olyan sikeresen, mint János. A két Bolyai számelméleti kutatásai azonban eddig nem váltak közkinccsé. Nemcsak hogy Gausshoz, a legkompetensebb bíróhoz nem jutottak el, de rajtuk kívül senki más nem tudott ezekrõl, immár 140 éve. A Teleki-téka polcain hevertek napjainkig. Feltárva azokat elmondhatjuk, hogy az elsõ magyar matematikus, aki a számelmélet terén jelentõs eredményeket ért el: Bolyai János.
A fentiekben Bolyai János vizsgálódásairól számoltunk be. Közben mindegyre felmerült Bolyai Farkas neve is. Írásunk is azt példázza, hogy ez a két név szorosan összefonódik. Valóban lehet-e Bolyai Farkasra emlékezni anélkül, hogy Jánosra, a fiúra ne gondolnánk, és írhatunk-e Jánosról úgy, hogy közben az apáról megfeledkezünk? Németh László szerint: "Ezt a két embert... nemcsak példátlan heves apa-fiú viszony s az azonos és egymásra utaló foglalkozás kapcsolta össze, hanem egy és ugyanazon probléma, az emberi agyban felmerültek közt tán a legmegdöbbentõbb, megoldásában a legcsodálatosabb".
Arról, hogy Bolyai János életének melyik szakaszában foglalkozott számelmélettel, már P. Stäckelnél olvashatunk. Szerinte Farkas már a 30-as években biztatta Jánost, hogy próbálkozzék e kérdéskör vizsgálatával, s õ mint ifjú behatóan tanulmányozta a Disquisitiones arithmeticae-t. Bolyai János tehát már egészen korán találkozott a számelmélettel, s azt egész életén át mûvelte. Azon kevés kéziratlap közül, amelyen keltezés is van, az egyik (1842. április 24-én Domáldra címzett levélre írt sorok) például arról árulkodik, hogy õt a "domáldi remeteség" idején is foglalkoztatták a számelmélet problémái. A fentiekben leírt eredményeit azonban az 1850-es évek közepén érte el. Legalábbis ezeket fõképpen az 1854-55-ös években keletkezett levelekben találhatjuk meg [5], [7]. Ekkor Bolyai János már elég idõs volt. A számelmélet terén végzett munkái is beszédes cáfolatai néhány szerzõ véleményének, akik szerint János alkotóképessége már korán kimerült, vagy hogy lanyhult volna érdeklõdése a matematikai kérdések iránt. Példáink is bizonyítják, hogy éppen ellenkezõleg, Bolyai János utolsó éveiben is tiszta fejjel gondolkozott matematikai problémákon, a matematikai kutatás örömét akkor sem hagyta abba.
Reméljük, hogy írásunk
szerény tisztelgés Bolyai János születésének
közeledõ 200. évfordulója elõtt,
aláhúzván azt a Benkõ Samu-i igazságot,
amely szerint Bolyai "élete végéig megõrizte
a gondolkodás örömét".
IRODALOM
[1]
Stäckel, Paul: Bolyai Farkas és Bolyai János
geometriai vizsgálatai, Budapest, 1914.
[2] Dávid Lajos: A két
Bolyai élete és munkássága, Gondolat,
Budapest, 1979.
[3] Alexits György: Bolyai János
világa, Akadémiai Kiadó, Budapest, 1977.
[4] Weszely Tibor: Bolyai János
matematikai munkássága, Kriterion Könyvkiadó,
Bukarest, 1981.
[5] Kiss Elemér: Fermat's
theorem in János Bolyai's manuscripts, Mathematica Pannonica,
Leoben-Miskolc-Triest, 6, 237-242 (1995).
[6] Sierpinski, Waclaw: Elementary
Theory of Numbers, Warszawa, 1964.
[7] Kiss Elemér: Bolyai János
vizsgálatai a 4m+1 alakú prímszámok
két négyzet összegére való felbontásáról,
Polygon, Szeged, 1996/2 (sajtó alatt).
[8] Kiss Elemér: A "Bolyai-ládák''
legújabb titkai, Természet Világa, 125,
405-408 (1994)
 |
Természettudományi és tudománytörténeti dokumentumok |