
Fig. 1. Torsion balance used in Eötvös' measurements
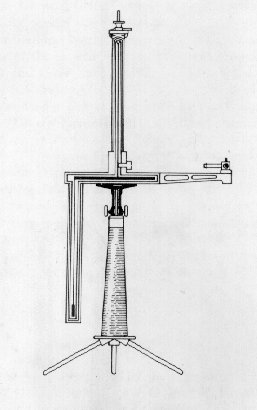
Fig. 2. Sketch of the torsion balance
(Received 31 August 1990)
Roland Eötvös' classic experiment
concerning the proportionality of inertial and gravitating masses,
performed at first in 1889, has again become the focus of scientific
interest in the 1980's, due to the possibility of the existence
of a Fifth Force, as proposed by Fischbach and coworkers. The
publication of Eötvös, Pekár and Fekete omitted
various details of their experiment which may be relevant for
the re-interpretation of their results. The aim of this report
is to fill in some of these details, and to discuss the impact
of the Eötvös experiment on modern research.
"Ars longa, vita brevis"
Inspired by the beauty of the Newtonian system, Baron Roland von Eötvös experimentally investigated the proportionality of inertial and gravitating masses in 1889, and reported his results in the Proceedings of the Hungarian Academy in 1890 [1]. In this work he improved Bessel's accuracy 1/60 000 to 1/20 000 000. This was a short report of 3 pages. Inspired by this achievement, the Royal Scientific Society of Göttingen in 1906 offered a prize (see Appendix I) for the following task:
"A very sensitive method was given by Eötvös to make a comparison between the inertia and gravity of matter. Considering this and the new development of electrodynamics as well as the discovery of radioactive substances, Newton's law concerning the proportionality of inertia and gravitation is to be proved as extensively as possible."
Eötvös began a series of investigations with his co-workers Pekár and Fekete in the years 19061909. This included data taking through approximately 4000 hours. Eötvös personally reported his results at the l6th International Geodesic Conference in London in 1909 [2], quoting an achieved accuracy of 1/100 000 000. The complete work of Eötvös, Pekár, Fekete was submitted to the Beneke Foundation in 1909 [3]. Its motto was "Ars longa, vita brevis" (the art lasts long, life lasts short), which is indeed a true characterization of the fate of Eötvös' work. The evaluation of C. Runge, Dean of the Faculty of Science in Göttingen [4] says that Eötvös has quoted an accuracy of 1/200 000 000, but since the submitted text does not include the real theoretical discussion of the observational data, the Faculty recommends only a reduced prize for this work (3400 German Marks instead of 4500 Marks). In Appendix I we reprint the text of this evaluation.
Shortly thereafter the First World War came. Roland Eötvös died in 1919, and the detailed description of the experiments performed in 19061909 was published by his assistants Pekár and Fekete only in 1922 [5]. This is the text known, cited, and translated by the international scientific community worldwide. When the collected works of Roland Eötvös were published by the Hungarian Academy of Sciences [6], the editor (Eötvös' former student P. Selényi) included some additions in parentheses [...] in the reprinted EötvösPekárFekete paper [5], taken from the original manuscript [3]. The original Benekeprize manuscript was lost somewhere in the hands of the heirs to Pekár and Selényi. The more complete text taken from the Volume [6] has been reprinted in English in Budapest in 1963 [5].
The Eötvös experiment was repeated
by J. Renner (a former student of Eötvös, and a physics
teacher in the famous Lutheran High School in Budapest where among
others J. von Neumann and E. P. Wigner studied). The results of
Renner's experiment were published in Hungarian [7] (with a German
abstract, reprinted in Appendix II). Renner claimed an empirical
accuracy of 1/2 000 000 000 to 1/5 000 000 000.
Acknowledging the basic role played by the connection between inertial mass and gravitating mass in General Relativity, P. G. Roll, R. Krotkov and R. H. Dicke carried out a new experiment, using modern technology, and achieved an accuracy of 1/100 000 000 000 [8]. Dicke and coworkers were able to increase the sensitivity compared to Eötvös in part by measuring the accelerations of their test masses to the Sun, rather than to the Earth as Eötvös had done. In such an experiment any signal arising from the difference between gravitational and inertial mass would have the same 24hour periodicity as the Earth's rotation. The advantage of such an approach from an experimental point of view is that it allows such a signal to be discriminated from background perturbations, without disturbing the torsion fibre. Of course, one must be careful to exclude other perturbations which will have the same 24hour period. In fact Eötvös, Pekár and Fekete were the first to compare the accelerations of different materials to the Sun, and for platinum versus mangalium they quote a fractional difference of 6 x 109. However, since no error is quoted and few other details of their analysis are presented, it is difficult to know precisely how the sensitivity of this part of their experiment compared with that of their more extensive work measuring accelerations to the Earth.
 Fig. 1. Torsion balance used in Eötvös' measurements |
 Fig. 2. Sketch of the torsion balance |
In analyzing the Eötvös results, Dicke expressed his polite doubts about the accuracy claimed by Eötvös' assistants. Among his concerns were the following:

Fig. 3. Data sheet from the R. Eötvös bequest
It should be emphasized that the analyses of both Dicke and Fischbach agree that the errors quoted by Eötvös, Pekár and Fekete are consistent with the statistical scatter of their data. Moreover, the confidence level of the best fit of Fischbach et al to the Eötvös data, viewed as suggesting a Fifth Force, is 86%, which is perfectly reasonable.
Let us quote Eötvös himself [5]:
"Ars longa, vita brevis. The admonition of this old saying
motivates the authors of this paper to compile the results of
their investigation and to submit them to the judgement of a high
scientific Aeropag. Methods of observation refine and improve
naturally in the course of observation, and hence no mortal could
close his work if without cease would follow the otherwise laudable
impetus to replace the useful by the even better."
Eötvös' experiment is one of the last pearls of the grand epoch of classical physics. At the end of their investigations [5] Eötvös, Pekár, and Fekete studied how far the proportionality of inertia and gravity is valid in case of radioactive materials. (This was already in the era of E = mc2.) The proportionality was verified for a 0.1 g sample of RaBr2 with an accuracy of 1/2 000 000.
In the following decades, the investigation of the structure of matter called attention to other possible forces of Nature beyond the longranged gravity and electricity, and beyond the shortranged nuclear and weak interactions. According to the quantum theory the range of the force (r) is related to the mass (m) of the quanta of the transmitting field by the quantum law r = h / mc, where h is Planck's constant and c is the speed of light.
The infinite length of the gravitational
and electric field lines is logically connected to the absolute
conservation laws of mass (energy) and charge. If there is any
further exact or approximate conservation law (e.g. the conservation
of the baryonic charge B, discovered by E. P. Wigner [10]),
it may be that a further unknown field exists which may transmit
a Fifth Force. But if the rest mass of the field quanta were exactly
zero (as in the case of photons), hot bodies would radiate these
quanta as well, in contradiction to thermodynamical experience.
Thus one may hypothesize that the field quanta should have a small
but nonvanishing rest mass (m), consequently the transmitted
Fifth Force would have a long but finite range (x0
= h / mc). This gives rise to a compositiondependent
"action at a distance" between two massive bodies, where
the interaction energy is the sum of the gravity and the Fifth
Force contributions:
For astronomical distances only Newtonian
gravity contributes,
For laboratory distances, however, one may
experience an "effective gravity"
with an effective gravitational constant
which may differ from the (astronomical)
Newtonian gravitational constant G. If B is the
baryon number (protons plus neutrons) in the atom, and if M
is the mass of the atom in hydrogen atom mass units mH ,
that is M = m / mH , then
with a = F / GmH2.
In the case of hydrogen B/M 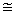 1, whereas for
carbon B/M = 1.00782, for copper B/M = 1.00895, and
for lead B/M = 1.00794. Hence the effective gravitational
constant, manifesting itself over laboratory scales may be composition
dependent. This idea can be checked by comparing the empirical
value of G on astronomical and laboratory scale, and by
testing its composition-dependence. Eötvös' experiments
contributed to both.
The torsion balance was used to measure any small difference
1, whereas for
carbon B/M = 1.00782, for copper B/M = 1.00895, and
for lead B/M = 1.00794. Hence the effective gravitational
constant, manifesting itself over laboratory scales may be composition
dependent. This idea can be checked by comparing the empirical
value of G on astronomical and laboratory scale, and by
testing its composition-dependence. Eötvös' experiments
contributed to both.
The torsion balance was used to measure any small difference

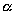 between gravitational accelerations of two substances.
Any significant difference would imply a composition-dependent inertial mass /
gravitational mass ratio.
Plotting
between gravitational accelerations of two substances.
Any significant difference would imply a composition-dependent inertial mass /
gravitational mass ratio.
Plotting  (
(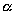 / g)
(where g is the gravitational acceleration) for the results published by
Eötvös-Pekár-Fekete [5] as a function of
/ g)
(where g is the gravitational acceleration) for the results published by
Eötvös-Pekár-Fekete [5] as a function of
 (B/M)
(see Fig. 4. based on the work of P. Király [19]), a linear
relationship may be suspected.
Fischbach and co-workers concluded that the slope of the
resulting line was (5.65±0.7) x 10-6,
which differs from the expected value of zero by several standard
deviations [11]. If the Fifth Force really exists with a range
of 100 m, say, the composition-dependence must be due to the action
of nearby mass distribution.
(B/M)
(see Fig. 4. based on the work of P. Király [19]), a linear
relationship may be suspected.
Fischbach and co-workers concluded that the slope of the
resulting line was (5.65±0.7) x 10-6,
which differs from the expected value of zero by several standard
deviations [11]. If the Fifth Force really exists with a range
of 100 m, say, the composition-dependence must be due to the action
of nearby mass distribution.
The Fifth Force hypothesis has had a double
effect: It has encouraged a series of modern experiments, and
it has increased the interest in details of the original Eötvös-Pekár-Fekete
experiment [5] (which seemed to indicate a positive effect).
Full lines in Fig. 4; represent error bars given by the
original authors, while dashed lines give increased statistical errors
suggested by P. Király. Results obtained in the environment of the
Renner experiment [7] apparently suggest a zero
result.
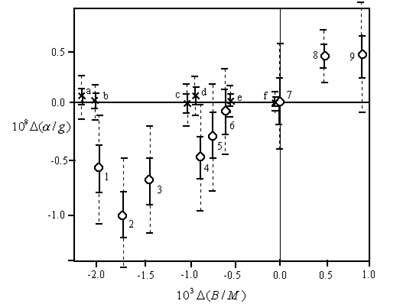
Fig. 4. Plot
of 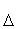 (
(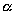 / g)
as a function of
/ g)
as a function of
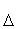 (B/M) [19].
In the EPF measurement: 1. tallow - Cu; 2. water - Cu; 3. CuSO4
solution - Cu; 4. CuSO crystals - Cu; 5. Asbestos - Cu; 6. snakewood
-Pt; 7. AgSO4
and FeSO4
(before and after the reaction); 8. mangalium - Pt; 9. Cu - Pt.
In Renner's measurement: a) paraffin - brass; b)
NH4F
- Cu; c) Bi - brass; d) Pt - brass; e) glass - brass; f) Mn-Cu
alloy - Cu. (The dashed lines show the increased statistical
scatter, as indicated in the text.)
(B/M) [19].
In the EPF measurement: 1. tallow - Cu; 2. water - Cu; 3. CuSO4
solution - Cu; 4. CuSO crystals - Cu; 5. Asbestos - Cu; 6. snakewood
-Pt; 7. AgSO4
and FeSO4
(before and after the reaction); 8. mangalium - Pt; 9. Cu - Pt.
In Renner's measurement: a) paraffin - brass; b)
NH4F
- Cu; c) Bi - brass; d) Pt - brass; e) glass - brass; f) Mn-Cu
alloy - Cu. (The dashed lines show the increased statistical
scatter, as indicated in the text.)
The authors of the present report do not
intend to enter the field of controversies related to the Fifth
Force, the interested readers may find references in the review
papers [e.g. 12]. Our only goal is to supply information about
the environments of the two classic Hungarian experiments. But
when doing so, let us keep in mind what Nieto, Goldman and Hughes
wrote [13]: "neither the concept of baryon number, nor the
mass defect existed at that time. Without these concepts, Eötvös
could have spent considerable time and effort in a fruitless attempt
to find out why the scatter in his data points was larger than
his error estimates. We can easily sympathize and imagine the
gnawing feeling that something was wrong, or that something very
important was being missed."
The Faculty of Science of the University of Budapest (carrying the name of Roland von Eötvös since 1950) is located in the downtown of Budapest, East of the Danube. The river follows a geological break: Its West shore abounds in steep hills (CaCO3, MgCO3), its East shore is flat (mostly wet sand deposit of the river). The East-West asymmetry is the dominating geological feature (Fig. 5).
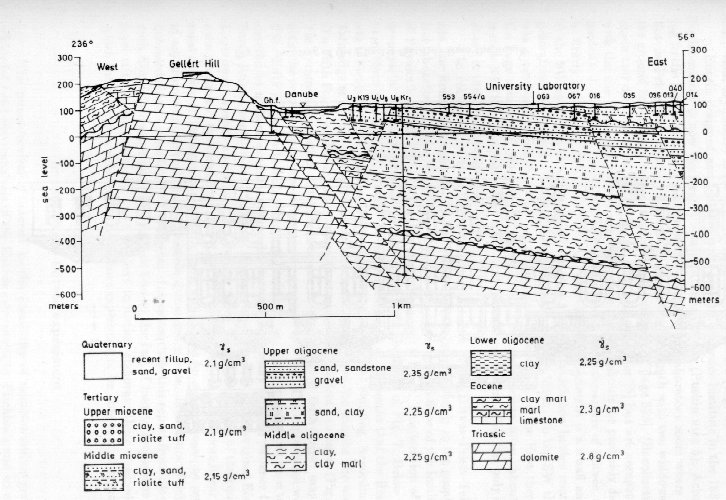
Fig. 5. Geological cross-section
between Gellért Hill and Eötvös University in Budapest
Eötvös designed and built the building of the Physics Institute in the 1880's; his laboratory is now the Department of Atomic Physics (Puskin utca 5). According to the Eötvös-Pekár-Fekete paper [6, page 328] the laboratory room where the Eövö-Pekár-Fekete experiment was carried out looks South with two windows on the ground floor; opposite to it there are tall buildings [6, page 328]. (Recollections made two decades later [13] contradict this original paper [5] but are compatible with the site of Renner's experiment, therefore this hint should be probably disregarded). J. Barnóthy joined the Institute 5 years after the departure of Eötvös, and he firmly locates the site of the Eötvös-Pekár-Fekete experiment is a small annex at the SW end of the building [14] (E on Figs 6 and 7), which now houses neutron generators. At Eötvös' time there was no building to the West. To the SW there was a temporary hole that was dug for future construction, to the East there is the huge complex of the Physics Institute with a strong concrete tower, about 20 meters NE (Fig. 8). Below the experimental room there was no cellar but only soil, above it there was no floor.

Fig. 6. Building of the Physics Institute from the South
In contrast to the highly asymmetric
location of the Eötvös-Pekár-Fekete site, the
Renner experiment was performed 25 years later, probably in the
geophysical laboratory, on the North side, in the middle of the
ground floor of the Institute of Physics building (about where
the computer room is now). This location of the geophysical laboratory
is given by G. Barta [15] indicated by R in Fig. 7. Below this room
there was a cellar, above it one additional floor, which means
that the Renner site is located rather symmetrically
(up-down, E-W) in the building. According to Talmadge et al [16],
the asymmetric location of the Eötvös site may be the
source of a Fifth Force, explaining the positive (composition-dependent)
outcome (Fig. 8). The symmetric position of the Renner site R
(compensated Fifth Force) may explain the zero (composition-independent)
outcome (Fig. 8). The explanation works if the Fifth Force exists
with a range of 10-50 meters. These conclusions have to be checked
by modern experiments by observers who are ready to learn patience
from Baron Roland von Eötvös. (G. Barta, who is presently
repeating the original Eötvös Experiment, speaks about
2 days of waiting before one single reading of the equilibrium
position of the torsion balance [17]). Eötvös selected
the best (most linear and most sensitive) Tungsten wires which
hung with weight for several years, to get rid of any distorting
internal tension. Eötvös demanded thousands of hours
of patient unbiased observations from his assistants. Let us conclude
this report from the past with Eötvös' message [5]:
"The authors bow to the fate of human limitations and leave
it to future times and future workers to further elaborate those
observations which they themselves believe upon mature experience
to be able to still improve."
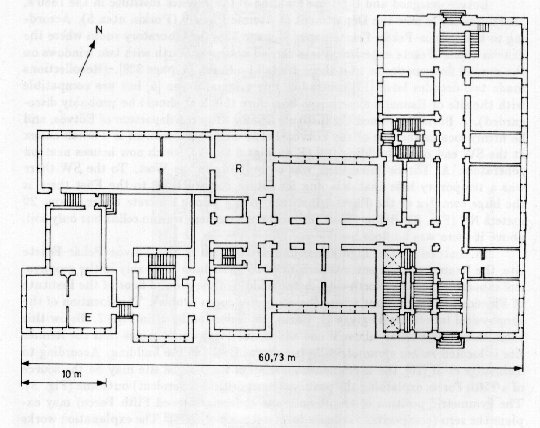
Fig. 7. Ground plan of the building
The recent revival of interest in the possibility of non-Newtonian gravity, which followed the reanalysis of the Eötvös experiment by Fischbach and co-workers [11,12] owes much to the perception that the experiments of Eötvös, Pekár, and Fekete were carefully done and hence deserve to be taken seriously. The widespread favorable view of this series of experiments is due in part to the detailed description of their experiment contained in the published literature, and in part to other details of their experiment which we know of from personal communications [9,14,15,17], and from aspects of their methodology that we can infer from various sources. The following are two additional examples of some of the details of their experiment which were not described in their paper. The torsion balances used in the experiment were mounted on stone piers (approximately one meter on a side) which were sunk deep into the ground.
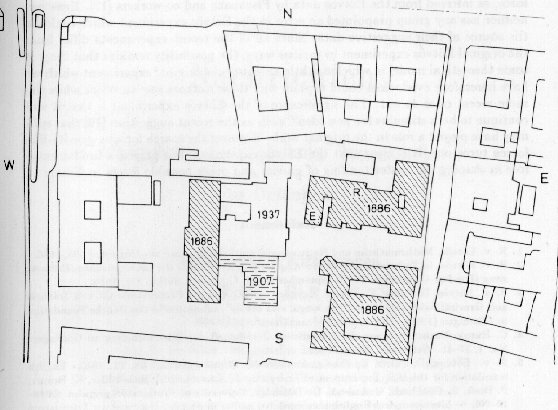
Fig. 8. Campus
The
purpose of these piers was to provide a stable shock-free platform
for the sensitive balances, and a number of these are still visible
today at the Atomic Physics Institute. Another interesting example
deals with their comparison of the reactants before and after
the chemical reaction
Ag2SO4 + 2FeSO4 —>
2Ag + Fe2(SO4)3.
Since the Ag produced by this reaction precipitates out of the liquid, the center-of-mass of the initial reactants would not coincide with that of the final products. If the difference of the centers of mass were not corrected for, then it would couple to local gravity gradients and produce a large (but spurious) signal which could simulate a violation of Equivalence Principle [12]. In fact Eötvös and co-workers found that the accelerations of the reactants before and after the chemical reaction were the same, which is what we expect in all theories. This indicates that the authors were evidently careful to correct for this effect, although the details of their methodology are not provided.
It has now been approximately five years
since the classic work of Eötvös, Pekár and Fekete
stimulated interest in the possibility of a fifth force. During
this period numerous experiments have been carried out, and many
are still under way. To date these experiments have not confirmed
the original suggestion of a fifth force, as inferred from the
Eötvös data by Fischbach and co-workers [12]. However,
neither has any group pinpointed an error in the Eötvös
experiment which could be the source of their suggestive data.
Since all of the recent experiments differ from the original Eötvös
experiment in various ways, the possibility remains that there
is some theoretical model in which a subtle aspect of the original
experiment which we have heretofore overlooked could explain why
those authors saw an effect while the more recent ones do not.
The significance of the Eötvös experiment is that it
will continue to be a stimulus for new ideas, such as the recent
suggestion [18] that spin may have played a role in the original
work. However the search for new gravity-like forces turns out,
it is clear that the Eötvös experiment has played a
fundamental role in shaping our understanding of gravity and other
possible forces in Nature.
___________________
Dedicated to Prof. J. Csikai on his
60th birthday
 |
Eötvös home page |